Parallele Algorithmen

In diesem Kapitel betrachten wir die Parallele Ausführung von Algorithmen. Bisher haben wir als Beispiele vor allem trivial parallelisierbare Probleme genommen bei denen eine große Anzahl an unabhängig zu bearbeitbaren Teilproblemen anfallen. Wir gehen zuerst auf Ineffizienzen ein, die bei der parallelen Lösung von allgemeineren Probleme, auftreten können. Danach betrachten wir ein Modell wie einzelne Berechnungsschritte in generischen Programmen zusammenhängen. Daran illustrieren wir die Schwierigkeit generische Berechnungen zu parallelisieren - insbesondere durch automatisierte Verfahren. Einfacher wird es, wenn wir ein Programm aus Berechnungsmustern zusammensetzen, die eine fixe Struktur mit bekannten Parallelisierungsmöglichkeiten haben. Ein Ansatz hierfür betrachten wir im Abschnitt “Datenparallelismus”. Hochperformante Berechnungsmuster haben meist als Bedingungen, dass viele Teile parallel berechnet werden können (Parallelität) und möglichst wenig Kommunikation zwischen den einzelnen Teilen notwendig ist (Lokalität). Im Abschnitt “Quellen der Parallelität und Lokalität” sehen wir, dass viele praktische Probleme diese Eigenschaften aufzeigen. Anschließend greifen wir einige beispielhafte Berechnungsmuster auf, gehen auf deren Anfälligkeit für die genannten Ineffizienzen ein und illustrieren Lösungen.

Ineffizienzen bei parallelen Algorithmen

Die Eigenschaften von effizienten parallelen Algorithmen versuchen wir zu erreichen indem wir die im Folgenden aufgelisteten Ineffizienzen vermeiden.

Ineffzienz	Beschreibung	Illustration
Schlechte sequenzielle Performance	Parallel ausgeführt werden einzelne sequenzielle Stränge. Wenn diese ineffizient sind, dann wirkt sich das aufs gesamte Problem aus. Diese Themen haben wir bereits adressiert, z.B. durch eine Cache-freundliche Verarbeitungsreihenfolge.
Geringer paralleler Anteil	Amdahl’s Gesetz zeigt uns, dass sequenzielle Teile des Programms einen starken Einfluss auf den Performancegewinn durch Parallelisierung haben.
Synch-Overhead	Berechnungen werden zwar parallel ausgeführt aber nur für kurze Zeit bevor sie wieder zusammengeführt werden. Dies erzeugt a) Overhead für die Synchronisationsmechanismen und b) muss an jedem Synchronisationspunkt auf das langsamste Teilproblem gewartet werden.
Kommunikation	Die Bewegung von Daten ist oftmals eine größere Performancelast als die eigentliche Berechnung. Wenn Daten zwischen verschiedenen Teilproblemen ausgetauscht werden, dann erhöhen sich die Kosten für die Datenbewegung häufig um ganze Größenordnungen, z.B. weil der Hauptspeicher statt dem Cache oder das Netzwerk statt des Hauptspeichers benutzt werden muss. Man spricht von geringer Lokalität der Teilprobleme.
Load Imbalance	Bei ungleich über die Teilprobleme verteilter Komplexität kommt es zu einer Load Imbalance. In Konsequenz sinkt die Auslastung des Systems und damit die erzielbare Performance
Mehrarbeit durch Parallelisierung	Durch die eigenständige Ausführung der gleichen Berechnung in verschiedenen Teilaufgaben, kann ggfs. ein höherer Parallelisierungsgrad erreicht und/oder der Synchronisations-/ Kommunikationsaufwand minimiert werden. Je nach verfügbaren Ressourcen, Problemstruktur und Ziel (z.B. Energie statt Zeit minimieren) kann der Mehraufwand die Vorteile überwiegen.

Parallelität in Algorithmen

Trivial parallelisierbare Probleme lassen sich einfach in eine große Anzahl an unabhängig zu bearbeitbaren Teilproblemen anfallen. Dafür gibt es überraschend viele nützliche Anwendungen, z.B.:

• Monte Carlo Simulationen

• Verschlüsselung und Komprimierung, wenn die Daten hierzu in unabhängige Blocks zerlegt werden

• (Brute-Force) Knacken von Verschlüsselungen

• Bildverarbeitung: Farbkonvertierung, Maskierung, Skalierung, Rotation

• Einige Operationen der linearen Algebra: Addition, Multiplikation mit Skalarwert

Wenn wir generischere Probleme betrachten, dann haben wir Abhängigkeiten zwischen einzelnen Berechnungsschritten. Diese können wir als Directed Acyclic Graph (DAG) darstellen. Betrachten wir beispielsweise die Berechnung der relativen Gewichtung der Elemente eines Arrays der Größe 4:

sum = a[0]
sum += a[1]
sum += a[2]
sum += a[3]
a[0] = a[0] / sum
a[1] = a[1] / sum
a[2] = a[2] / sum
a[3] = a[3] / sum

Der entsprechende Graph dazu ist:

Fig. 4 DAG relative Gewichtung Array

Anhand des Graphs können wir zwei Größen berechnen:

• \(T_1\): die zu verrichtende Arbeit, d.h. die auszuführenden Operationen. Hier: 8 (entsprechend der Code-Zeilen)

• \(T_\infty\): die minimale Anzahl an Schritten, wenn wir unendlich viele Prozessoren haben, d.h. die Länge des kritischen Pfades. Hier: 5 (entsprechend der rot markierten Kanten)

Nun können wir die Parallelität berechnen als durchschnittliche Operationen pro Schritt: \(T_1 / T_\infty\), hier: 1.6 Wie wäre die Laufzeit un Auslastung bei p Prozessoren?

p	Laufzeit	Auslastung
1	8	100%
2	6	(100% + 33%) / 2 = 67% = 8 / (2 * 6)
3	6	(100% + 2 * 16%) / 3 = 44% = 8 / (3 * 6)
4	5	(100% + 3 * 20%) / 4 = 40% = 8 / (4 * 5)
5	5	(100% + 3 * 20% + 1 * 0%) / 5 = 32% = 8 / (5 * 5)

Diese Laufzeit ist natürlich nur theoretisch unter folgenden Annahmen:

• Jede Operation dauert gleich lang

• Es gibt keinen Overhead für Kommunikation und Synchronisation

Um Programme automatisiert zu parallelisieren, könnten wir nun also für beliebige sequenzielle Programme einen DAG der Abhängigkeiten erstellen und dann die entsprechenden Teil parallel ausführen. Warum ist das in der Praxis schwierig?

Unabhängigkeiten in sequentiellen Code sind schwer erkennbar

Ein DAG für ein sequenzielles Programm lässt sich einfach bauen indem man jede Operation (jede Zeile) in Abhängigkeit zur vorherigen Zeile setzt. Dies hat den Vorteil, dass der Graph die Abhängigkeiten auf jeden Fall vollständig abdeckt. Der Nachteil ist, dass keinerlei parallele Abschnitte vorhanden sind.

Unabhängige Abschnitte sind schwer erkennbar, z.B.:

for(int i=1;i<n;i++) {
  b[i] = a[i-1];
}

Hier ist jeder der n-1 Schritte unabhängig voneinander - aber nur, wenn a und b auf unterschiedliche Speicherbereiche verweisen. Manchmal sind die Abhängigkeiten auch erst zur Laufzeit bekannt, z.B.:

void add_two_numbers(int data[N], int dst, int src1, int src2) {
  data[dst] = data[src1] + data[src2];
}

Unabhängigkeiten oft erst durch Code-Umformungen

Mit Domänenwissen kann es möglich sein den Code so umzuformen, dass das gleiche Ergebnis rauskommt aber mit weniger Abhängigkeiten und höherer Parallelität. Zum Beispiel könnten wir bei der relativen Gewichtung die Summenbildung so umformen:

sum_1 = a[0]
sum_1 += a[1]
sum_2 = a[2]
sum_2 += a[3]
sum = sum_1 + sum_2
a[0] = a[0] / sum
a[1] = a[1] / sum
a[2] = a[2] / sum
a[3] = a[3] / sum

Der entsprechende Graph dazu ist:

Fig. 5 DAG relative Gewichtung Array, Paralleler

Nun ergeben sich neue Werte:

• \(T_1\): 9 (entsprechend der Code-Zeilen)

• \(T_\infty\): 4 (entsprechend der rot markierten Kanten)

• Parallelität \(T_1 / T_\infty\): 2.25 Wie wäre die Laufzeit un Auslastung bei p Prozessoren?

p	Laufzeit	Auslastung
1	9	100%
2	5	(100% + 80%) / 2 = 90% = 9 / (2 * 5)
3	5	(100% + 60% + 20%) / 3 = 60% = 9 / (3 * 5)
4	4	(100% + 75% + 2 * 25%) / 4 = 56% = 9 / (4 * 4)

Solche Umformungen sind schwer automatisierbar durchfürbar. Hier wäre es noch relativ einfach, da wir eine Summe bilden und Addition assoziativ ist. Bei komplexeren Operationen haben wir diese mathematischen Eigenschaften meist nicht. Auch bei der numerischen Addition mit der begrenzten Genauigkeit von Fließkommazahlen ist Assoziativität nicht automatisch gegeben.

Partionierung des DAGs ist exponentiell schwierig

Jede einzelne Operation unabhängig auf einen anderen Prozessor zu verteilen ist nicht praktikabel, da sonst der Overhead für die Koordination, Synchronisation und Kommunikation zu hoch ist. Stattdessen wir eine optimale Aufteilung der Berechnungen gesucht mit folgenden Eigenschaften:

• Möglichst gleich große Arbeitspakete (Load Balancing)

• Möglichst wenig Abhängigkeiten zwischen den Paketen (Kommunikationsvermeidung)

Diese Definition wird schon theoretisch schwierig, da oft nicht bekannt ist wie teuer jede einzelne Operation ist und wie viele Daten pro Abhängigkeit ausgetauscht werden müssen.

Auch praktisch ist es schwierig, denn das Problem entspricht einer Graphpartionierung des Abhängigkeiten-DAGs. Graphpartionierung ist ein exponentiell schwieriges Problem. Die Auswirkung können Sie sehen, wenn Sie ein hinreichend großes C-Programm mit und ohne der -O3 Option übersetzen.

Datenparallelismus

Die automatische Parallelisierung von beliebigen sequenziellen Programmen ist also schwierig und erreicht nur wenig vom tatsächlichen Potenzial. Sequenzielle Programme haben aber für den Programmierenden Vorteile beim Schreiben und Debuggen, weil sie unserem Prozessdenken entsprechen. Ein Ansatz ist es wiederkehrende Berechnungsmuster zu verwenden:

• die einzelnen Berechnungsmuster können parallelisiert implementiert werden

• die Muster können sequenziell angeordnet werden, um das gewünschte Problem zu lösen.

Auf höchster Ebene lässt sich das durch die Nutzung von Programmbibliotheken umsetzen, die große Teilprobleme lösen, z.B. eine parametrisierte Simulation oder sämtliche Funktionen der Lineare Algebra.

Ein flexiblerer Ansatz ist Datenparallelismus bei dem wie gewohnt Operationen auf Variablen angewandt werden aber statt einzelne Werte als Operanden zu nehmen werden Arrays (/Vektoren/Matrizen) verwendet. Beispielsweise wird aus:

for(int i=0; i<n; i++) {
  c[i] = a[i] + b[i]
}

einfach: c = a + b mit der Bedeutung, dass a und b elementweise addiert werden.

Datenparallele Sprachen/Bibliotheken in unterschiedlichen Ausprägungen sind z.B. Spark, Tensorflow, NumPy, CUDA.

Neben den bekannten arithmetischen Operationen, die elementweise ausgeführt werden gibt es eine Reihe weiterer Operationen, die erst auf Arrays Sinn machen:

• Map: Anwenden einer Funktion auf jedes Element im Array. Dies sind die bekannten trivial parallelisierbaren Operationen, z.B. Multiplikation jedes Elements mit einer konstanten Zahl, berechnen des Hashwerts für jedes Array-Element

• Reduce: Zusammenfassen aller Elemente in ein Element durch wiederholtes Anwenden einer Funktion. Z.B. Berechnen der Summe aller Elemente: ((((a[0] + a[1]) + a[2]) + a[3]) + a[4]) + .... Insbesondere bei assoziativen Funktionen lässt sich die Berechnung parallelisieren (siehe oben, siehe unten).

• Selection/Stride: Auswahl einer Untermenge des Arrays nach einem Muster, z.B. Selektion jedes 3. Werts um die Rot-Werte aus einem RGB-Array zu selektieren

• Scatter/Gather: Verschiedene Bedeutungen, hier: Scatter, aufteilen eines Arrays in Unterarrays, die dann unabhängig bearbeitet werden können, z.B. Aufteilung RGB-Bild in R-, G- und B-Arrays. Gather: Einsammeln mehrerer Einzelwerte/Arrays in ein größeres Array

• Filter: Bilden eines kleineren Arrays mit Elementen, die ein Kriterium erfüllen

• Search: verschiedene Ausprägungen aber z.B. Rückgabe eines Arrays mit den Positionen von Elementen im originalen Array, die ein Suchkriterium erfüllen

• Sort: Sortieren der Elemente eines Arrays

• Scan: ähnlich zu Reduce aber alle Zwischenergebnisse werden behalten und als Elemente im Ergebnisarray gespeichert. Zum Beispiel bei + als Funktion auch bekannt als Prefix Sum: aus [0, 1, 2, 3] wird [0, 0+1=1, 0+1+2=3, 0+1+2+3=6].

INFO
Mehr Details zu Datenparallelismus, den einzelnen Operationen und deren Implementierung: Lecture 8, CS267 der UC Berkeley

Quellen der Parallelität und Lokalität

Egal mit welchem Ansatz ein Algorithmus parallelisiert wird - hohe Performance kann nur erreicht werden, wenn:

• viele Teile parallel berechnet werden können (Parallelität) und

• möglichst wenig Kommunikation zwischen den einzelnen Teilen notwendig ist (Kommunikationsvermeidung)

• die Kommunikation mit möglichst wenigen anderen Teilen notwendig ist (Lokalität)

Glücklicherweise zeigen viele praktische Anwendungen diese Eigenschaften, z.B.:

Parallelität

• Diskrete Simulationen: in jedem Zeitschritt kann jedes Objekt unabhängig voneinander berechnet werden. Die Interaktion findet über die Zeitschritte hinweg statt

• Suche kann in unterschiedlichen Teilbereichen parallel erfolgen

• Divide and Conquer: viele klassische Algorithmen zerlegen ein Problem in viele kleine Teilprobleme - diese können dann parallel gelöst werden

• Assoziative Operationen: Teilergebnisse können parallel berechnet werden und dann zusammengefasst

Lokalität

• Soziale Netze: jede Person ist nur mit einem kleinen Bruchteil aller Personen verbunden

• Web: jede Webseite wird nur von einem kleinen Bruchteil aller Webseiten verlinkt

• Diskrete Simulationen: jeder Zeitschritt ist nur vom vorherigen Zeitschritt abhängig

• Simulationen mit physikalischen Kräften: weiter entferne Objekte können ignoriert oder angenähert werden

• Convolution/Schablonen/Iterative numerische Lösungsmethoden für lineare Gleichungen: jeder Wert hängt nur von Werten in der direkten Umgebung ab

INFO
Mehr Beispiele in Lectures 5 und 6, CS267 der UC Berkeley

Beispiele: Ineffizienzen auflösen

Im Folgenden werden wir anhand von Beispielen zeigen wie die genannten Ineffizienzen vermieden werden können.

Geringer Paralleler Anteil: Problem paralleler machen als es ist

Bei einer N-Body Simulation werden viele Objekte simuliert zwischen denen Kräfte wirken. Zum Beispiel Sterne in einer Galaxie zwischen denen die Gravitation wirkt. Eine Parallelisierung ist möglich, wenn wir die Zeit als diskrete Größe behandeln. Das heißt, dass wir die Zeit in kleine diskrete Schritte unterteilen und nur für diese die Positionen, Beschleunigungen und Geschwindigkeiten der Sterne berechnen. Statt also mit beliebigen kleinen Zeiteinheiten umzugehen berechnen wir z.B. nur jede Sekunde. Dabei gehen wir davon aus, dass alle Objekte während der Zeiteinheit an konstanter Position verharren und am Ende der Zeiteinheit in ihrer neuen Position sind. Dies hat den Vorteil, dass wir das Update unabhängig für jedes Objekt berechnen können - die Updates der anderen Objekte interessieren uns dann erst wieder im nächsten Zeitschritt.

Ein weiteres Beispiel ist die Reduce-Operation. Beispielsweise berechnet die Summen-Reduktion die Summe aller Elemente in einem Array:

double sum = 0.0;
for(int i = 0; i < N; i++)
  sum += a[i]

Diese Berechnung ist vollständig sequenziell, da jede Operation sum += arr[i] von der vorherigen Operation sum += arr[i-1] abhängt. Dargestellt im linken Teil der folgenden Graphik. Stattdessen kann aber auch die Assoziativität der +-Operation ausgenutzt werden und Teilergebnisse parallel berechnet werden, wie im rechten Teil dargestellt:

Fig. 6 DAGs für sequenzielles und paralleles Reduce

Wir haben bereits erfahren, dass + zwar mathematisch assoziativ ist aber nicht unbedingt für Fließkommazahlen im Computer mit beschränkter Genauigkeit. Das parallelisierte Verfahren, wo immer paarweise aufaddiert wird hat aber gegenüber der rein sequenziellen Variante sogar noch den Vorteil von höherer numerischer Stabilität, weil tendenziell Werte mit gleicher Größenordnung miteinander addiert werden, also z.B.

• Einzelwerte mit Einzelwerte im ersten Schritt

• Summen von N/2 Werten im letzten Schritt Im sequenziellen Verfahren wird im letzten Schritt ein Einzelwert zur Summe von N-1 Werten addiert. Je nach Bandbreite der Zahlen und deren Anzahl kann der Einzelwert hier schon unterhalb der Genauigkeitsgrenze der Summe liegen und somit ignoriert werden.

Bei Reduce mit assoziativem Operator können wir also statt N sequenziellen Schritte auf \(log_2 N\) Abhängigkeiten reduzieren. Weitere assoziative Operatoren sind z.B.: Produkt, Min, Max, Mengenvereinigung.

Kommunikation optimieren: Convolution/Stencil/Zelluläre Automaten

Convolution ist eine Operation, die ein Input-Array auf ein Output-Array gleicher Größe abbildet. Dabei wir jedes Output-Element als gewichtete Summe des ursprünglichen Input-Elements an gleicher Stelle und einer fest definierten Menge an Nachbarelementen gebildet. Die Gewichte werden wiederum als Array dargestellt - dieses wird häufig Maske, Schablone/Stencil oder Convolution Kernel genannt. Beim zellulären Automaten wird in jedem Zeitschritt ein neues Array auf Basis des aktuellen Arrays berechnet, wo jedes Zielelement eine Funktion des entsprechenden Quellelements und dessen Nachbarschaft ist. Die Funktion kann hier andere Formen als die gewichtete Summe annehmen, z.B. beim Game of Life. Die Anwendungsgebiete sind breit:

• Bildverarbeitung, z.B. Unschärfe oder Kantenerkennung

• Simulationen mit zellulären Automaten, z.B. Nagel-Schreckenberg-Modell für Verkehrssimulationen

• Numerische Lösung von Differenzialgleichungen, z.B. Wärmeleitungsgleichung mit dem Crank-Nicolson-Verfahren

Jedes Zielelement kann unabhängig voneinander berechnet werden. Jedoch bestehen - im Gegensatz zu lächerlich einfach parallelsierbaren Problemen - Abhängikeiten im zeitlichen Verlauf, wenn die Berechnung mehrfach angewandt wird. Dies ist insbesondere bei Simulationen und numerischen Verfahren der Fall. Die Abhängigkeiten bedeuten, dass das Ergebnisse von einer parallelen Berechnung an eine andere Berechnung als Input kommuniziert werden müssen. Um die Kommunikation zu minimieren gilt es die Arbeit geschickt aufzuteilen.

Im Folgenden gehen wir durch ein Beispiel inklusive der Auteilung der Matrix auf verschiedene Threads und der Berechnung des entsprechenden Kommunikationsaufwands.

Nutzen Sie die Pfeiltasten (Links und Rechts) oder die folgenden Links, um durch die Visualisierung zu navigieren. Durch klicken oder berühren (Telefon/Tablet) können Sie auch zum nächsten Bild. Alternativ können Sie auch ein PDF mit allen Bildern runterladen. Zurück Vor

ÜBUNG: Arbeitsaufteilung

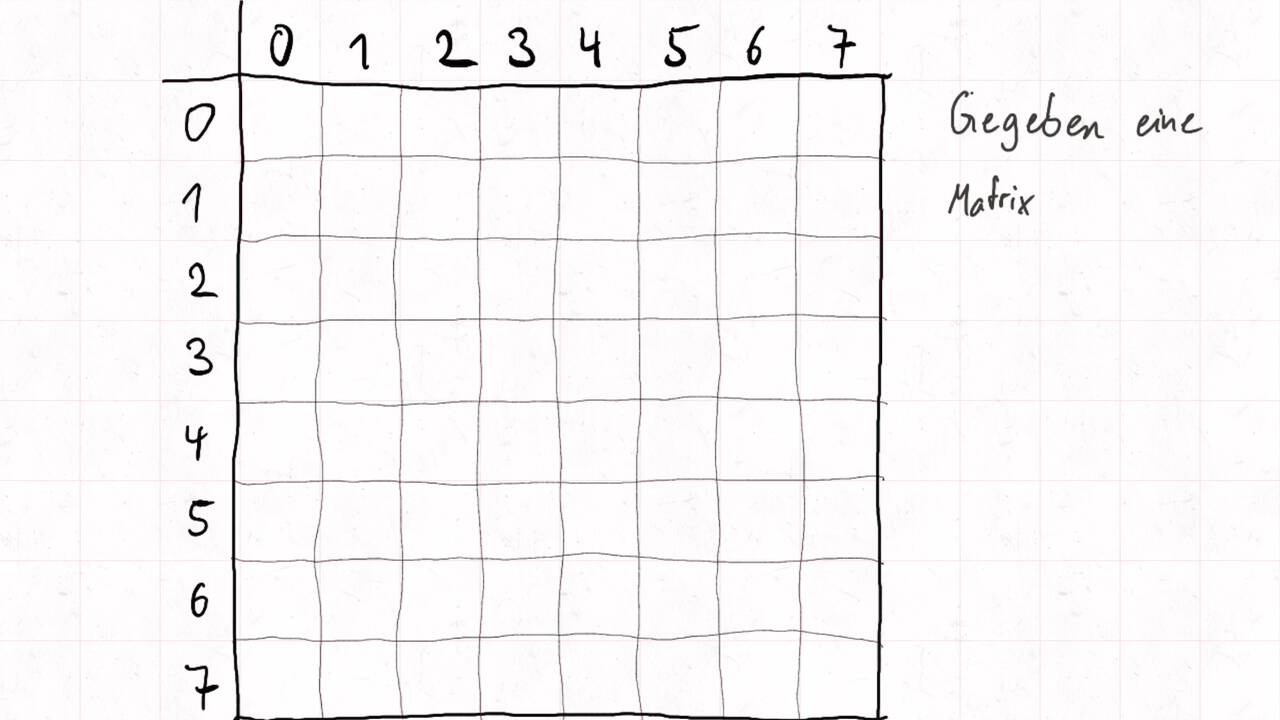
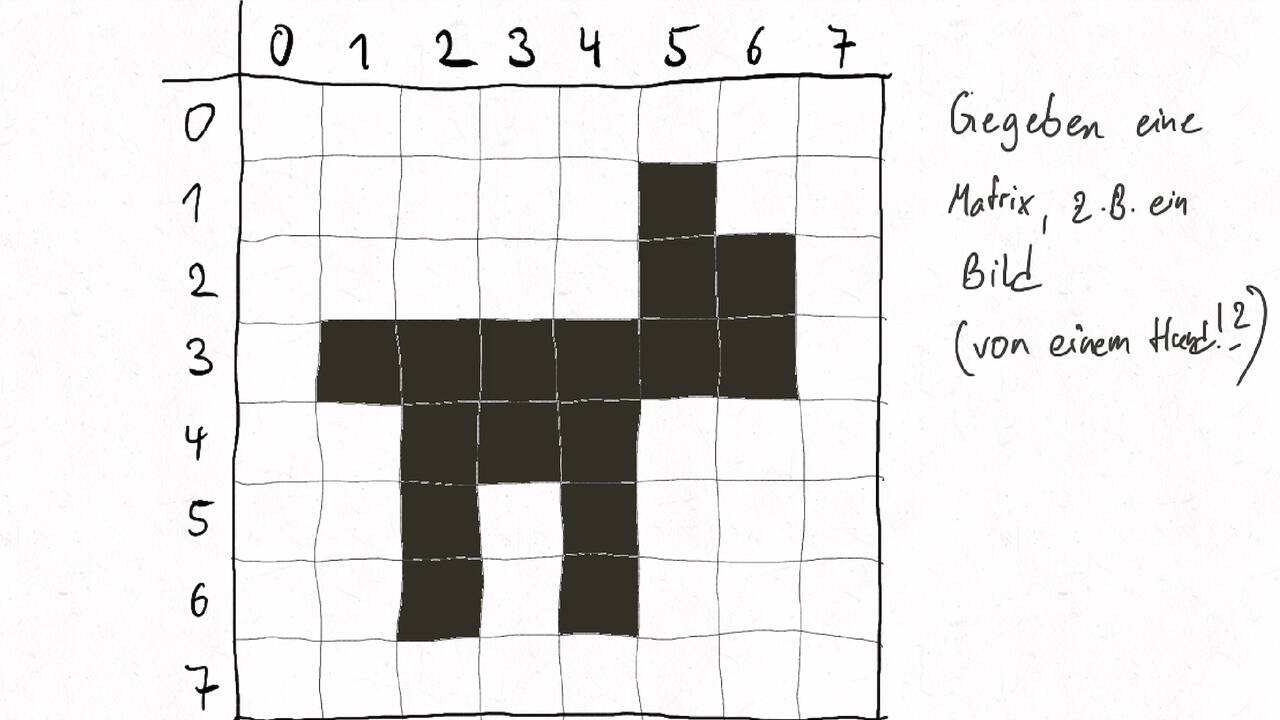
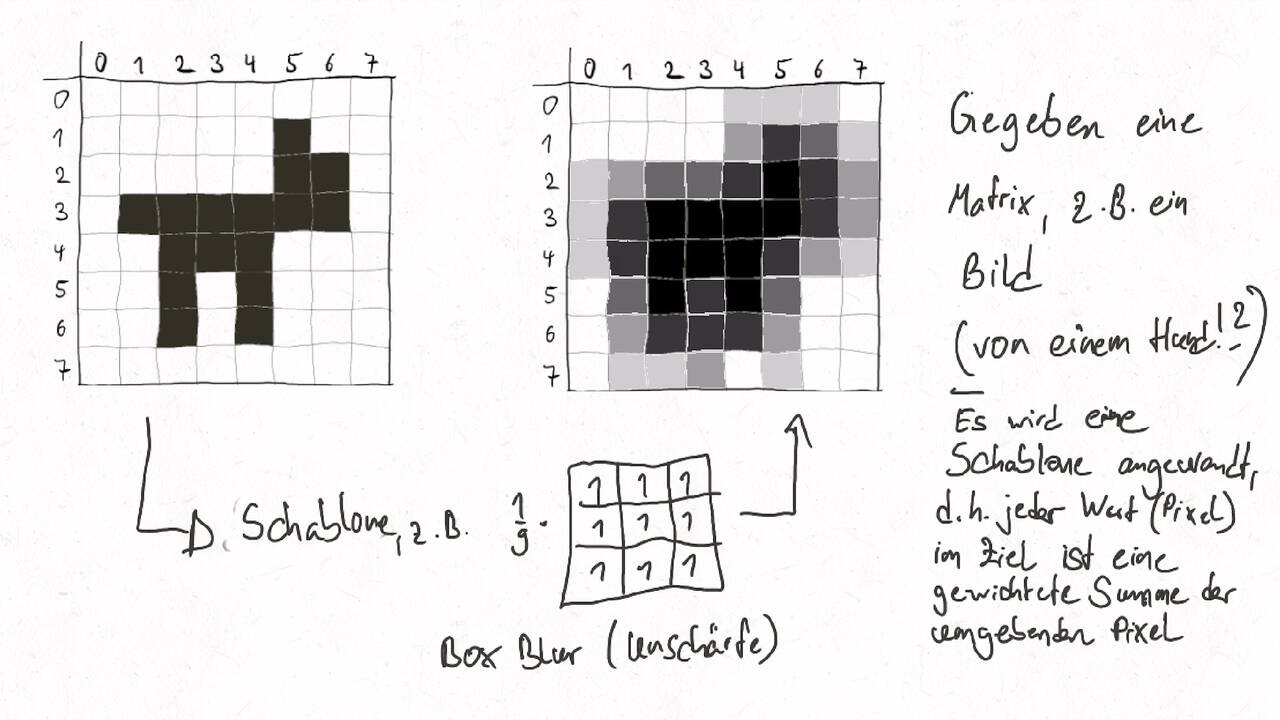
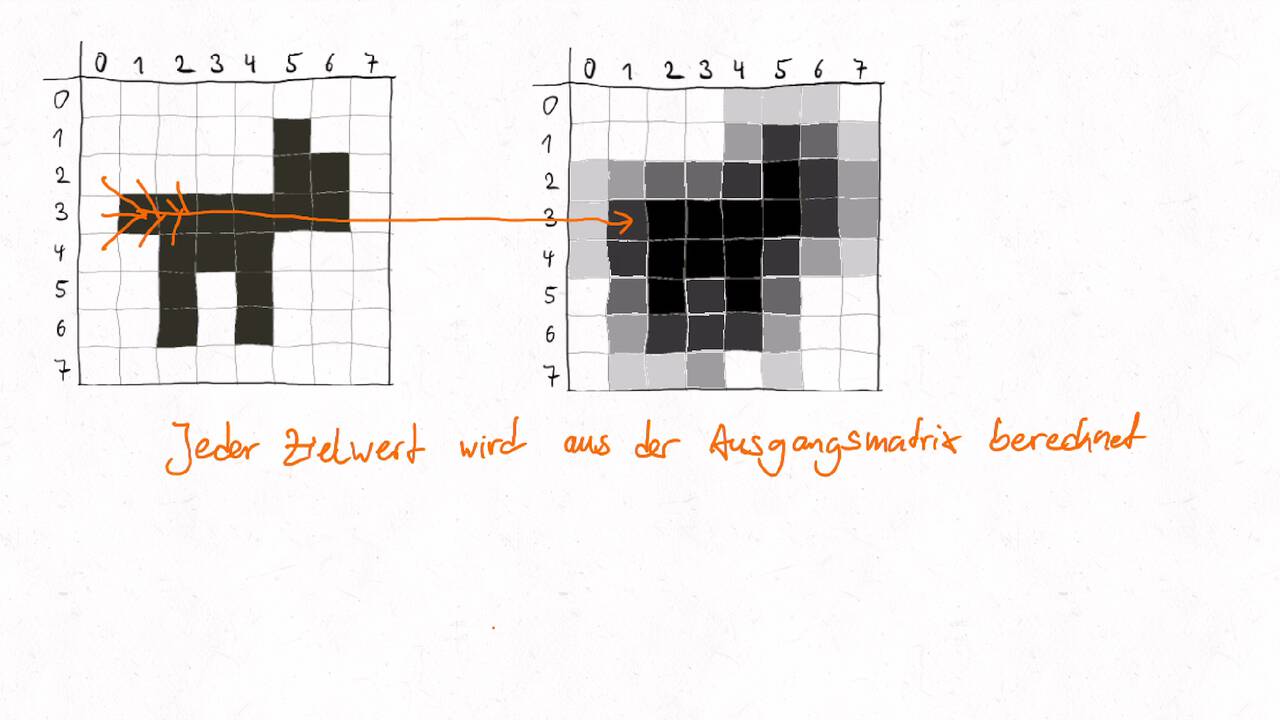
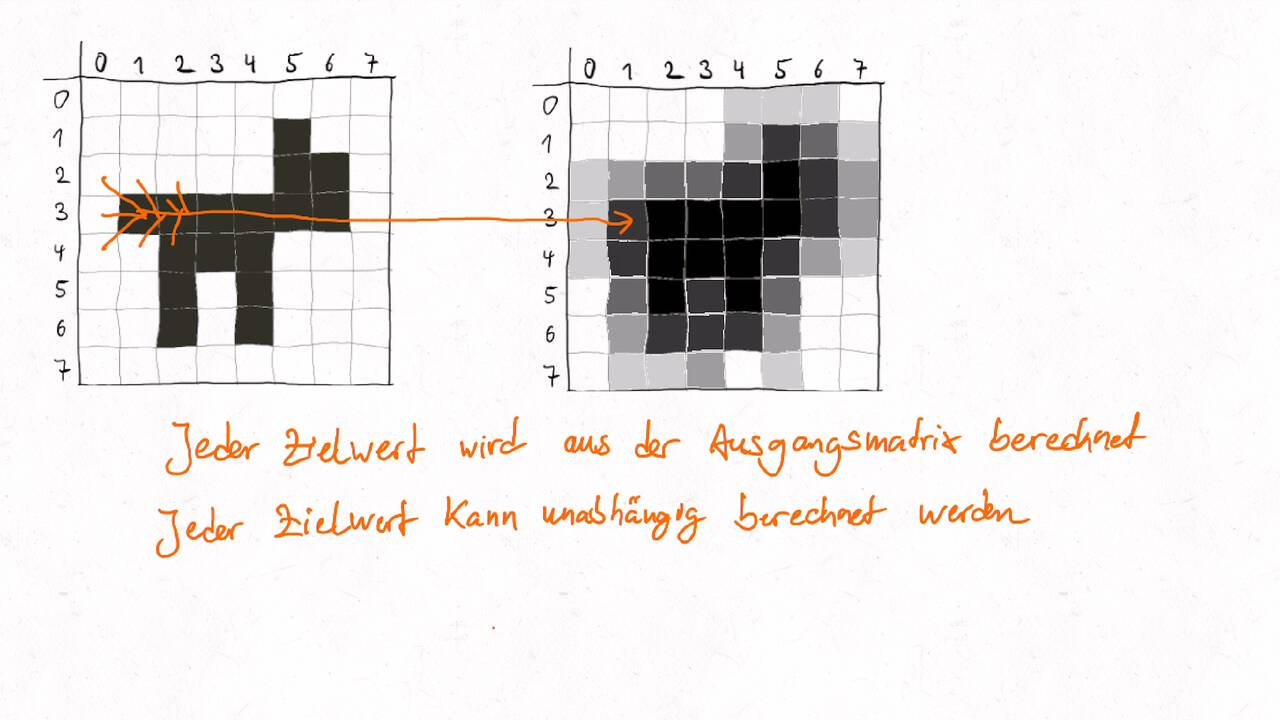
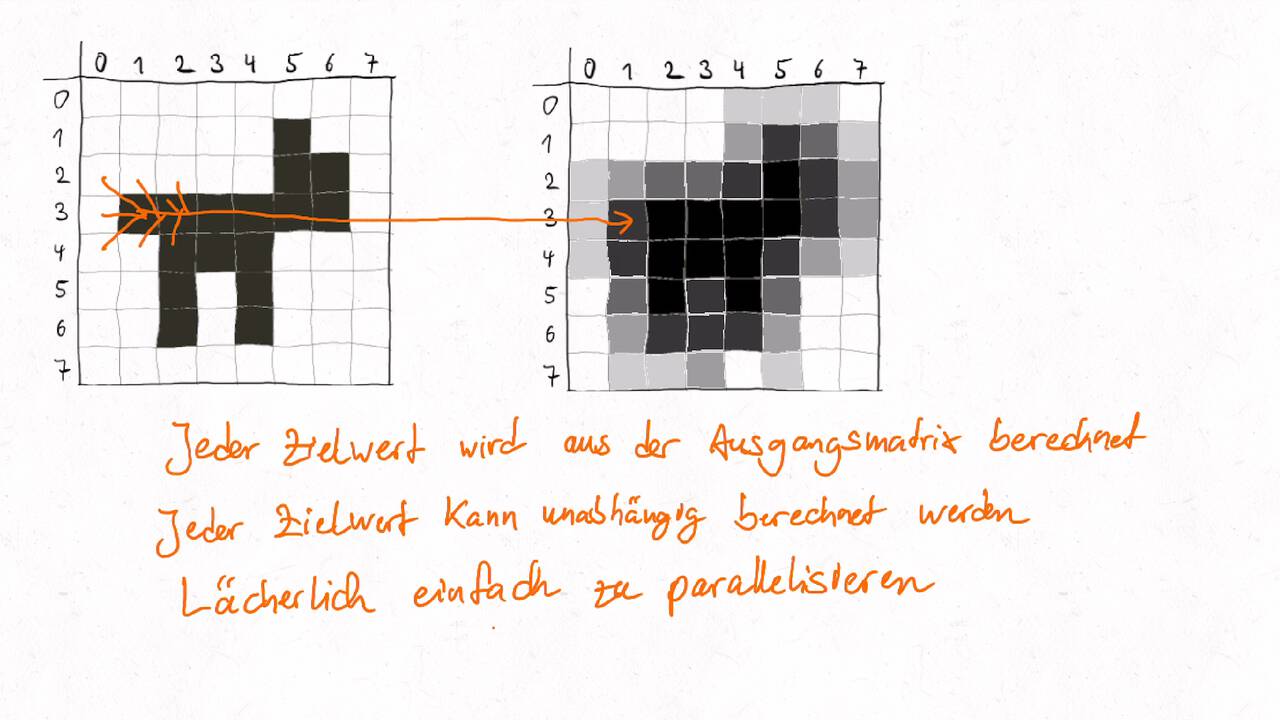
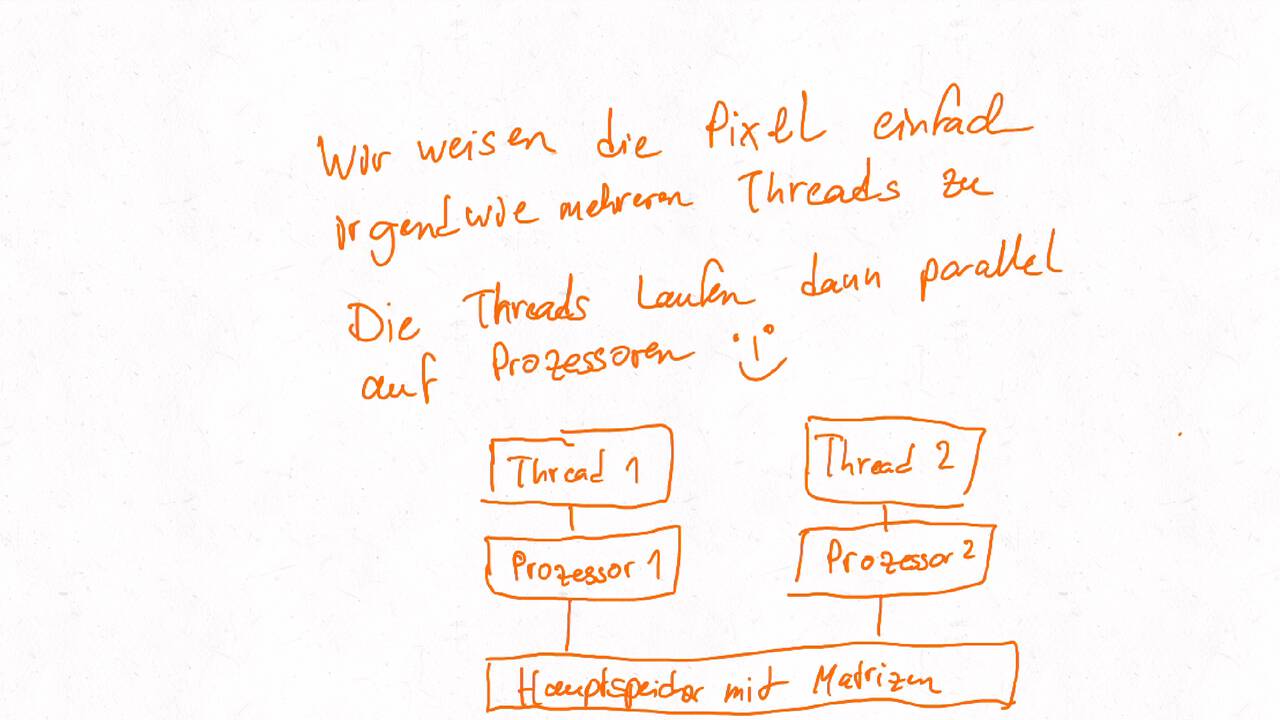
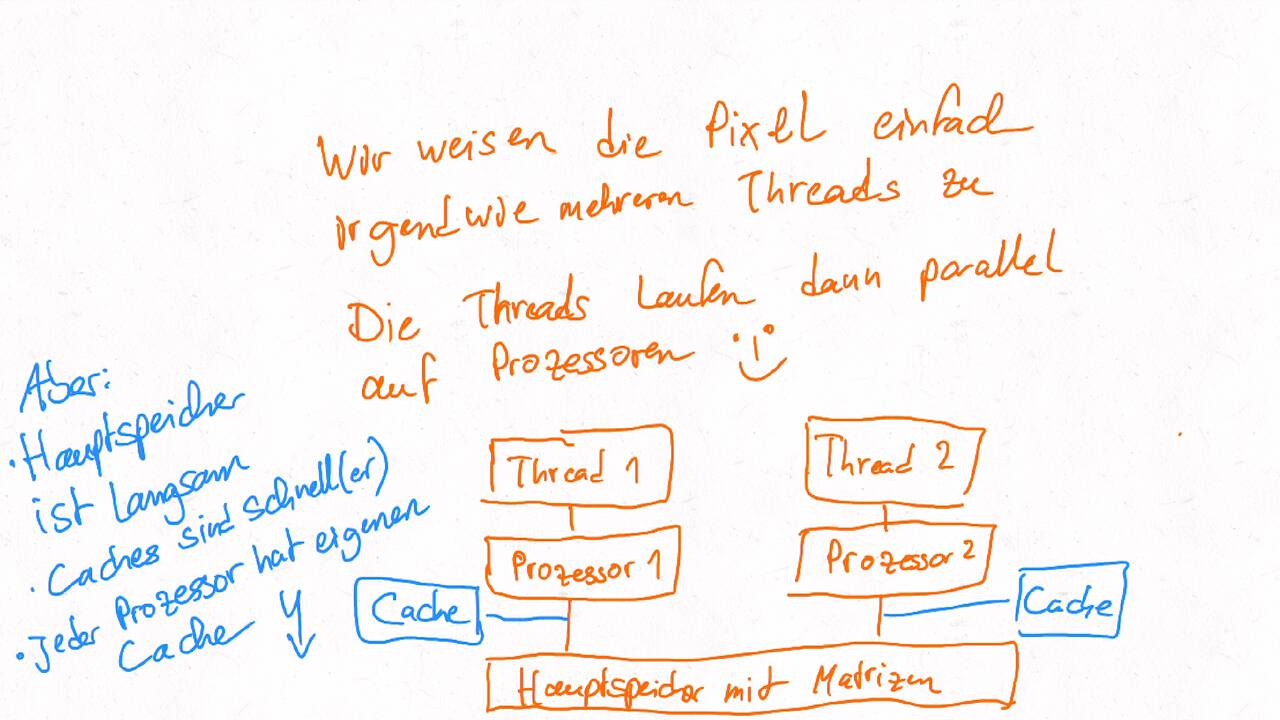
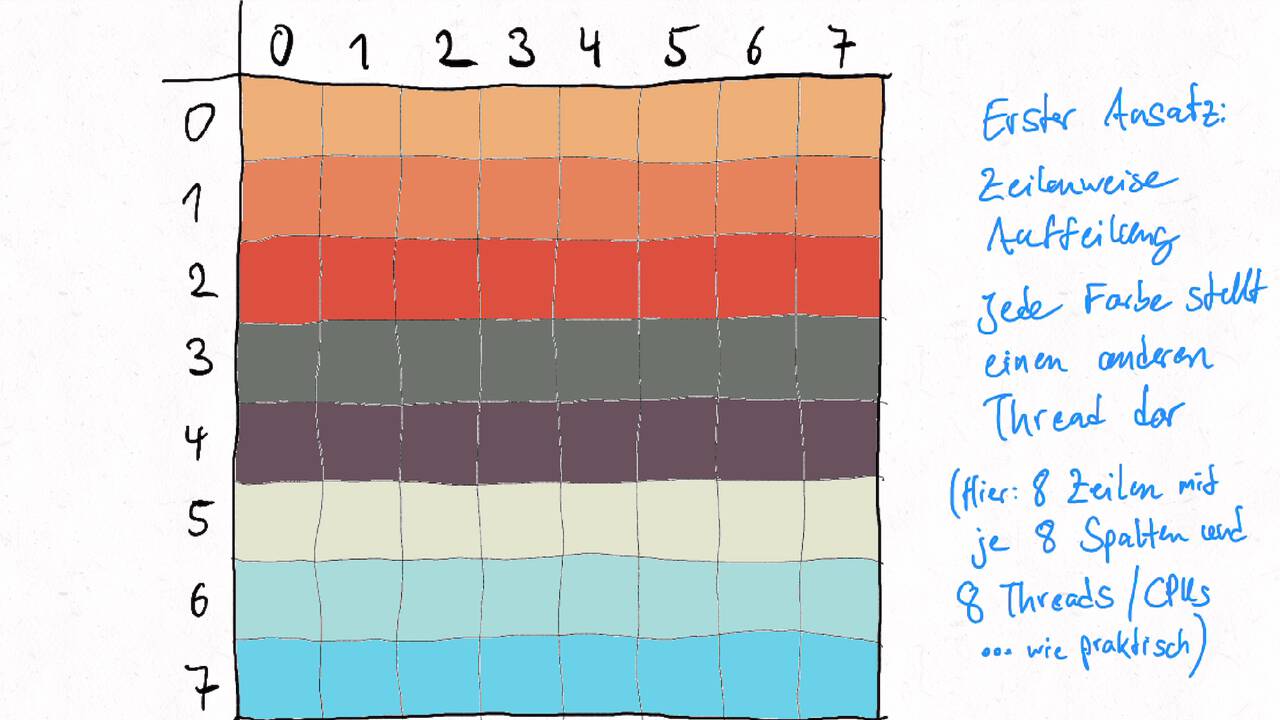
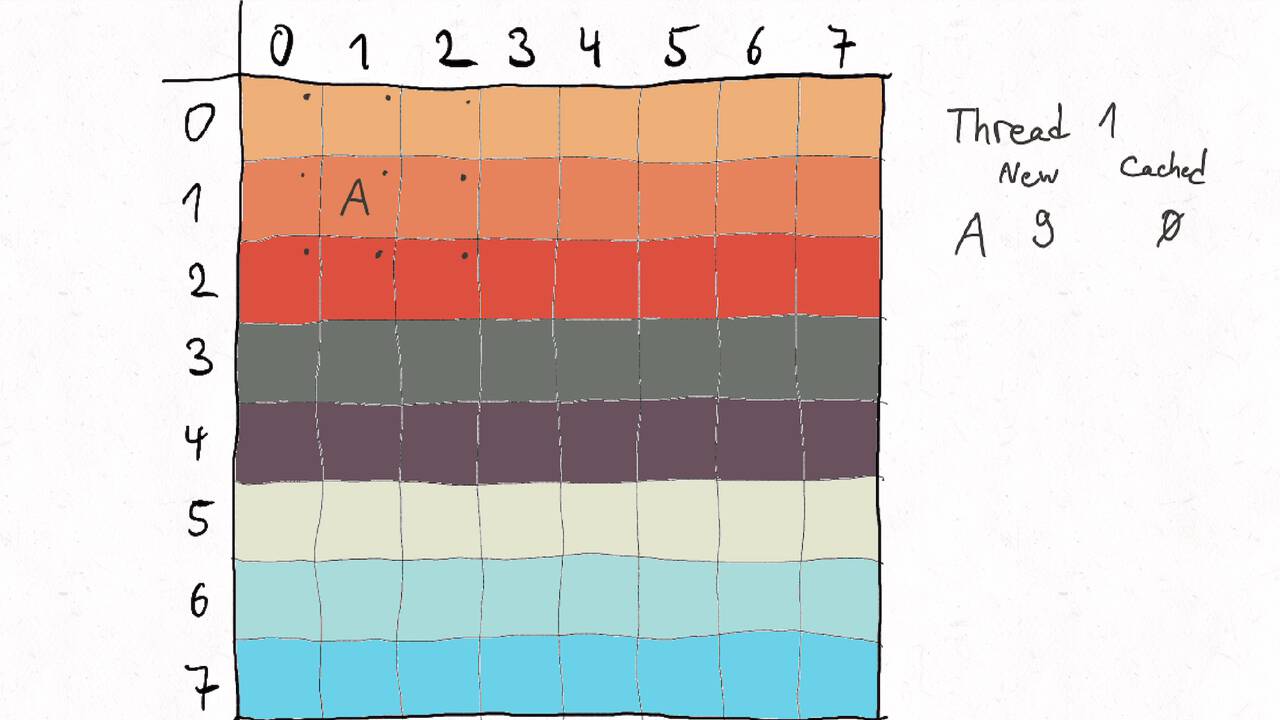
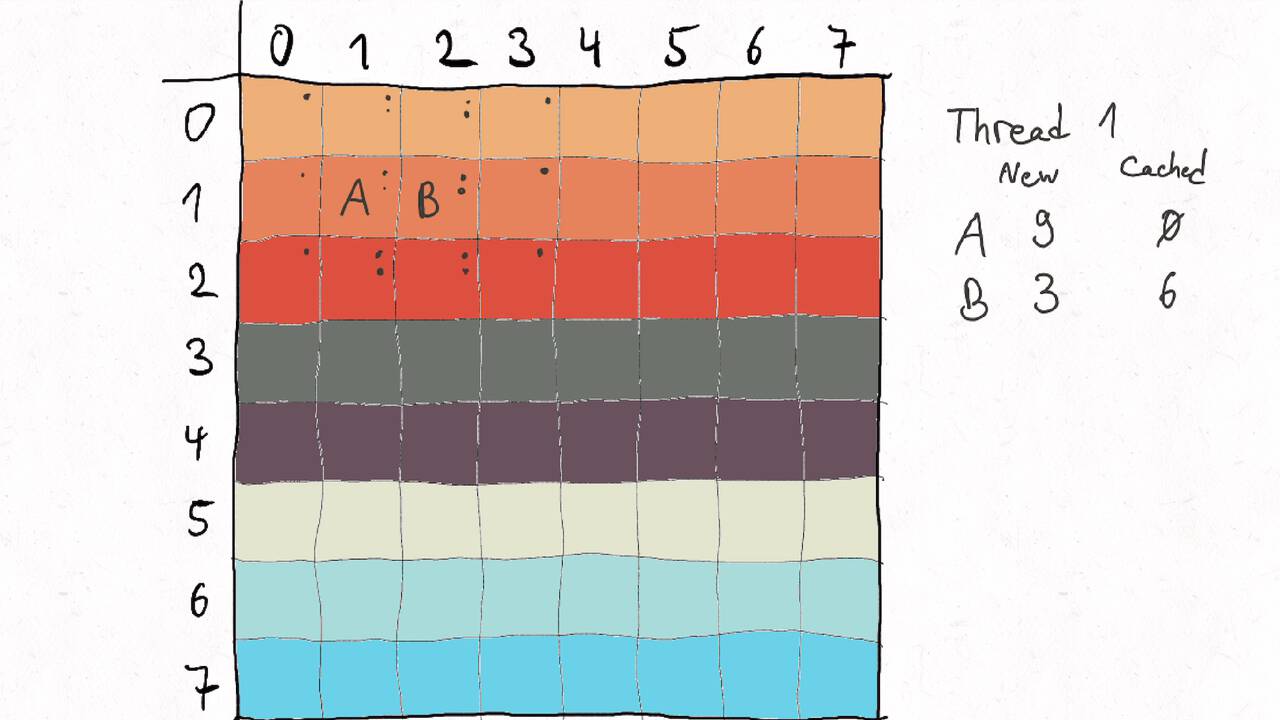
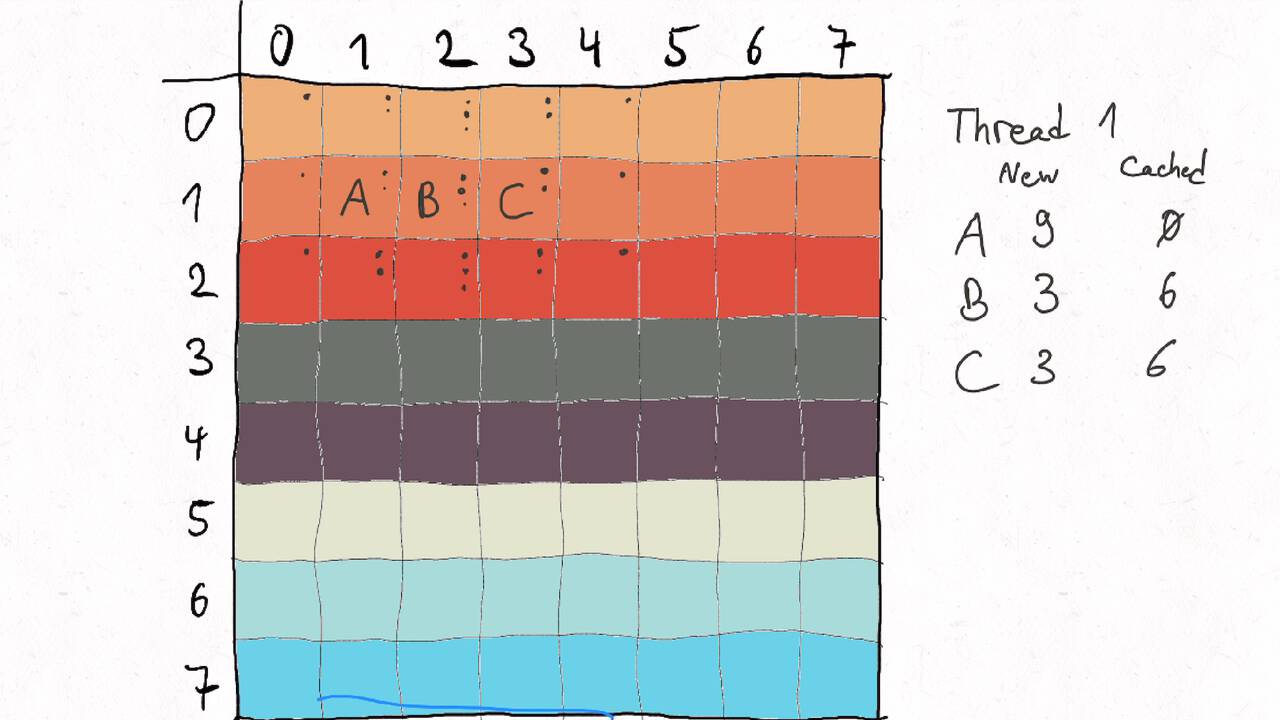
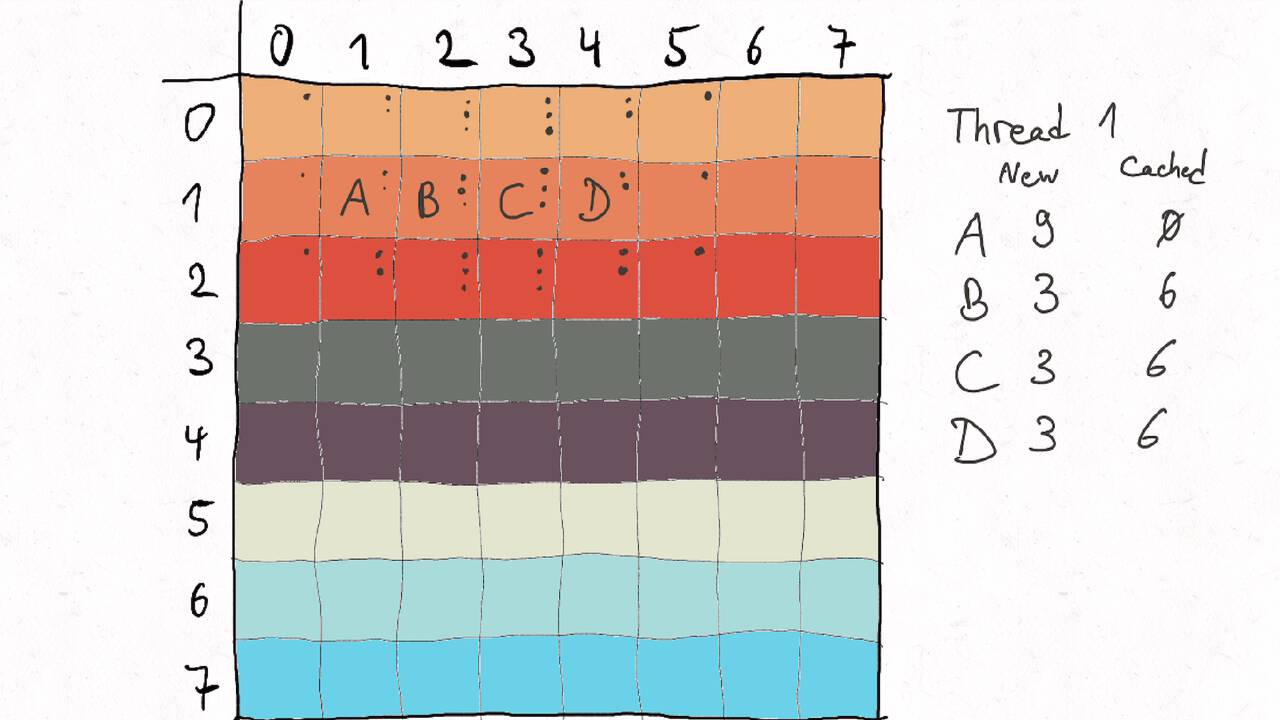
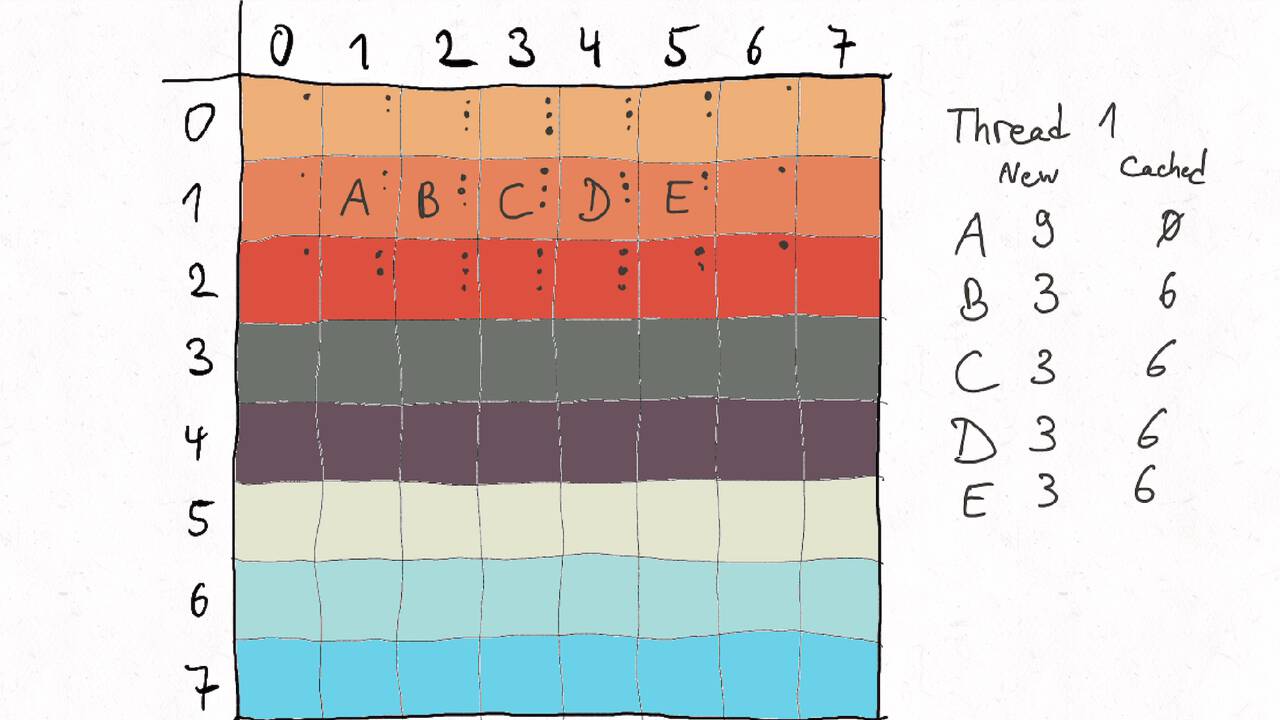
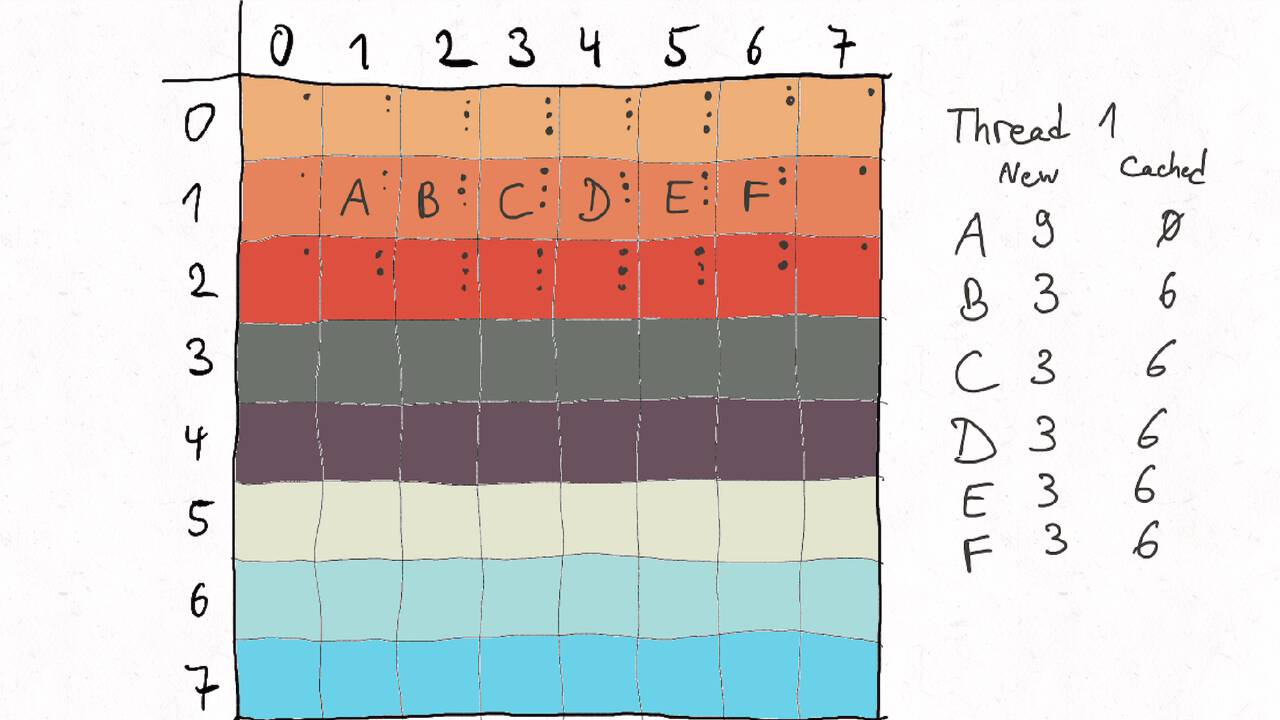
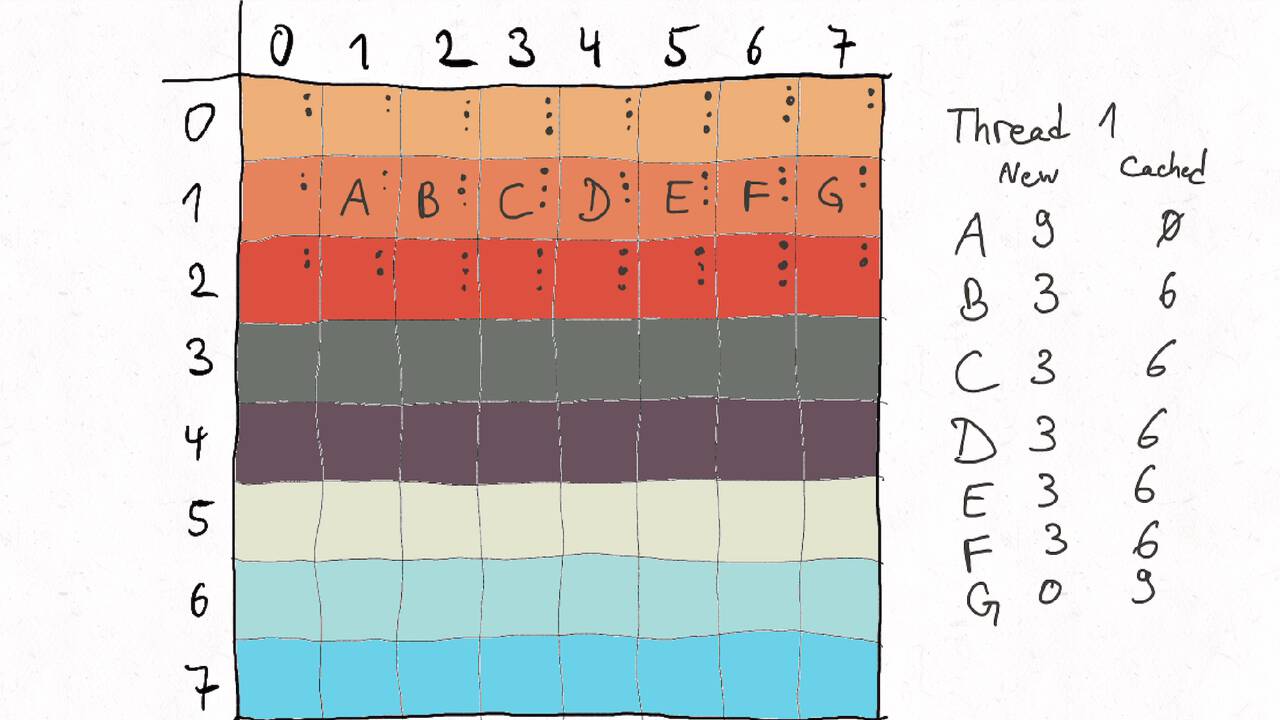
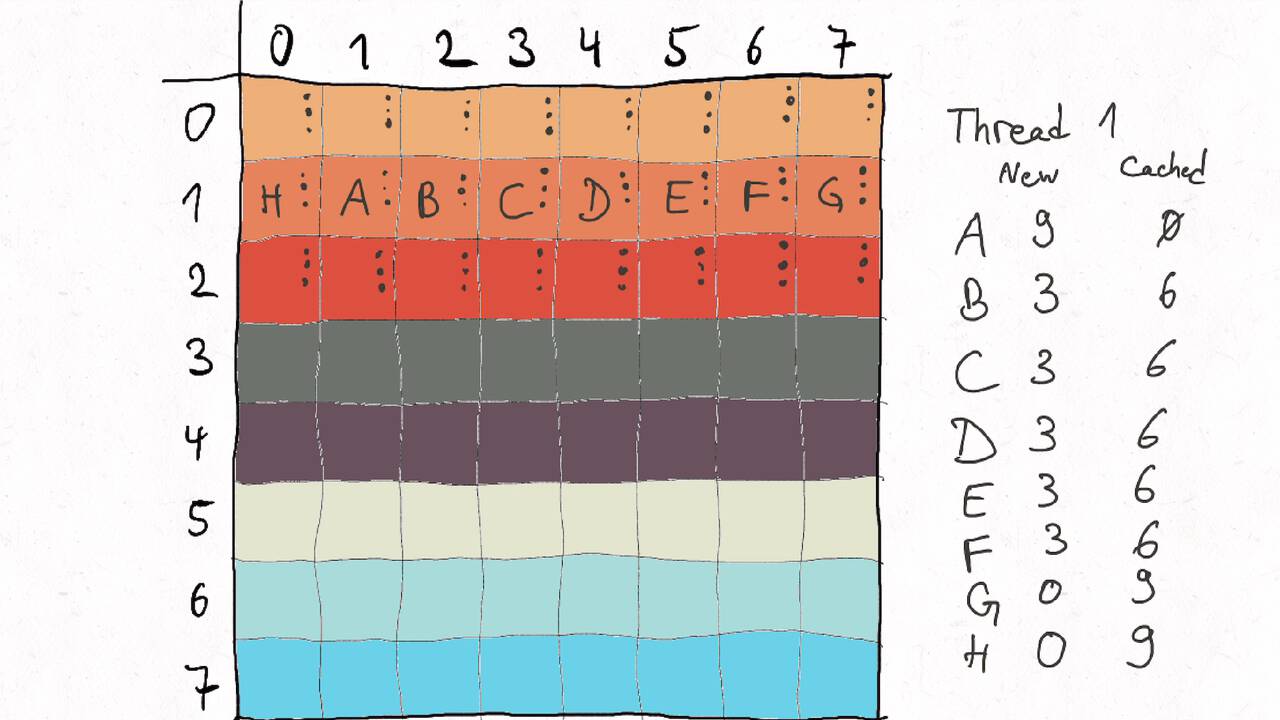
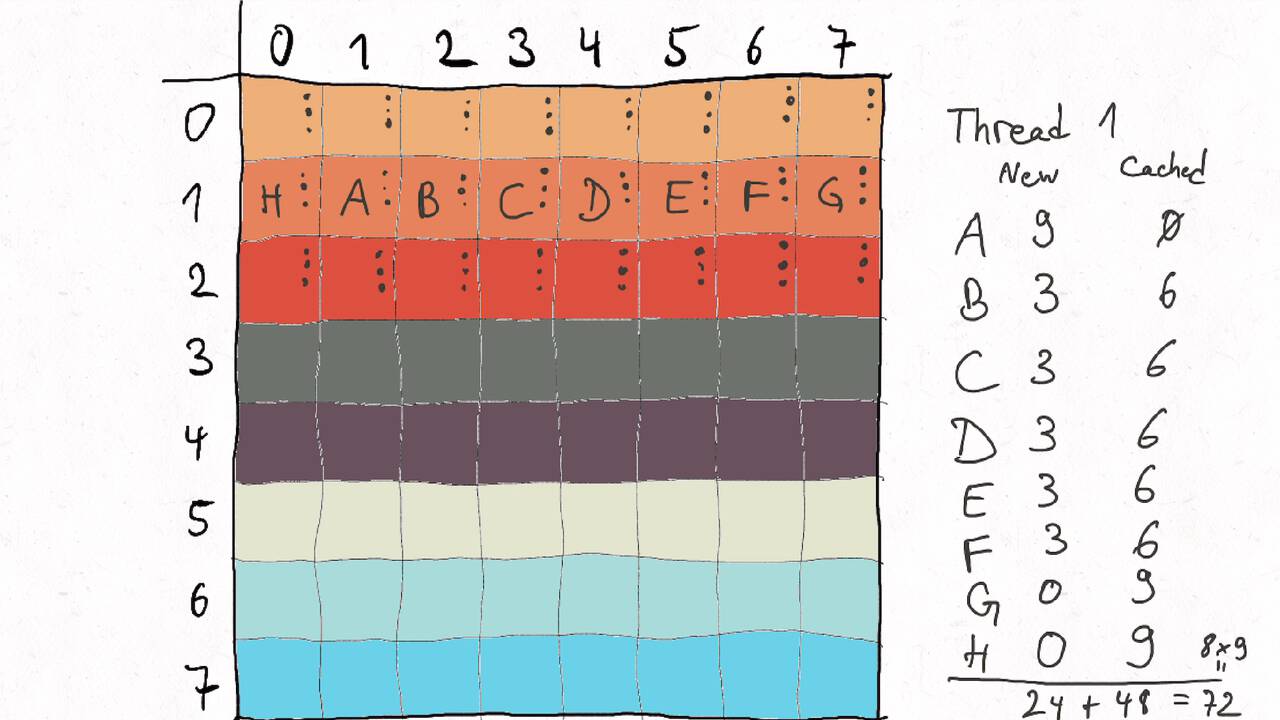
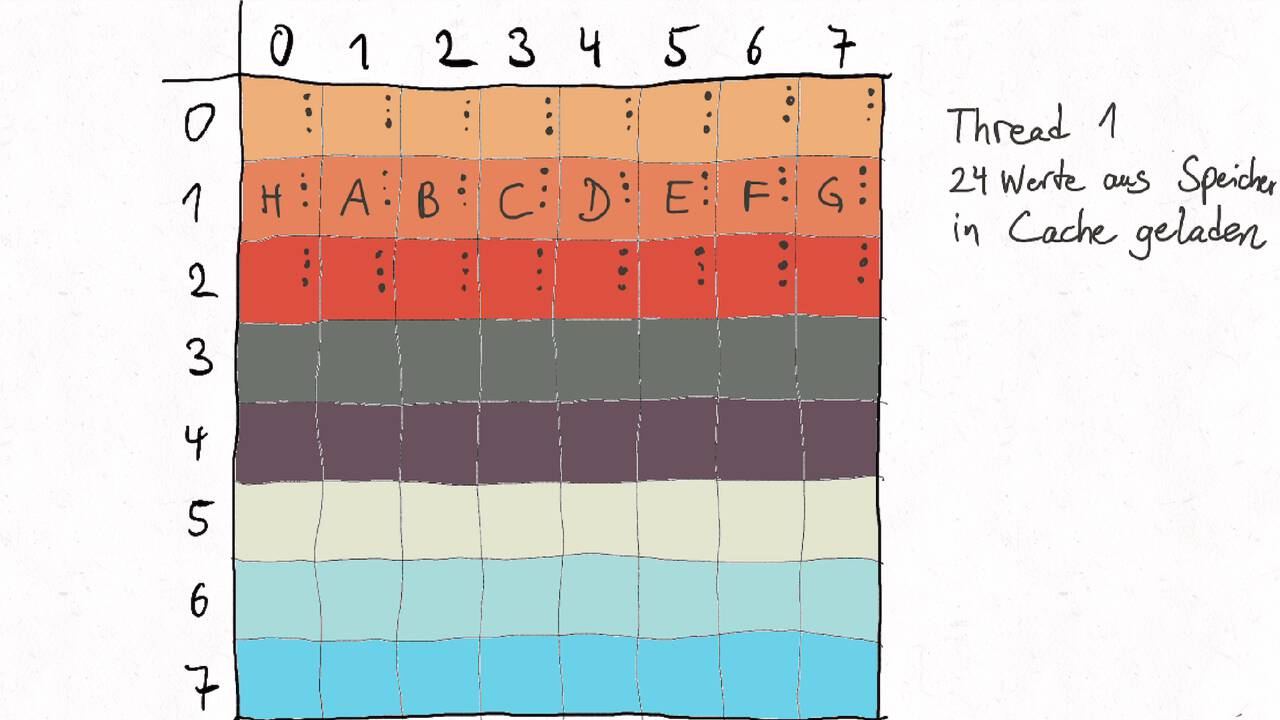
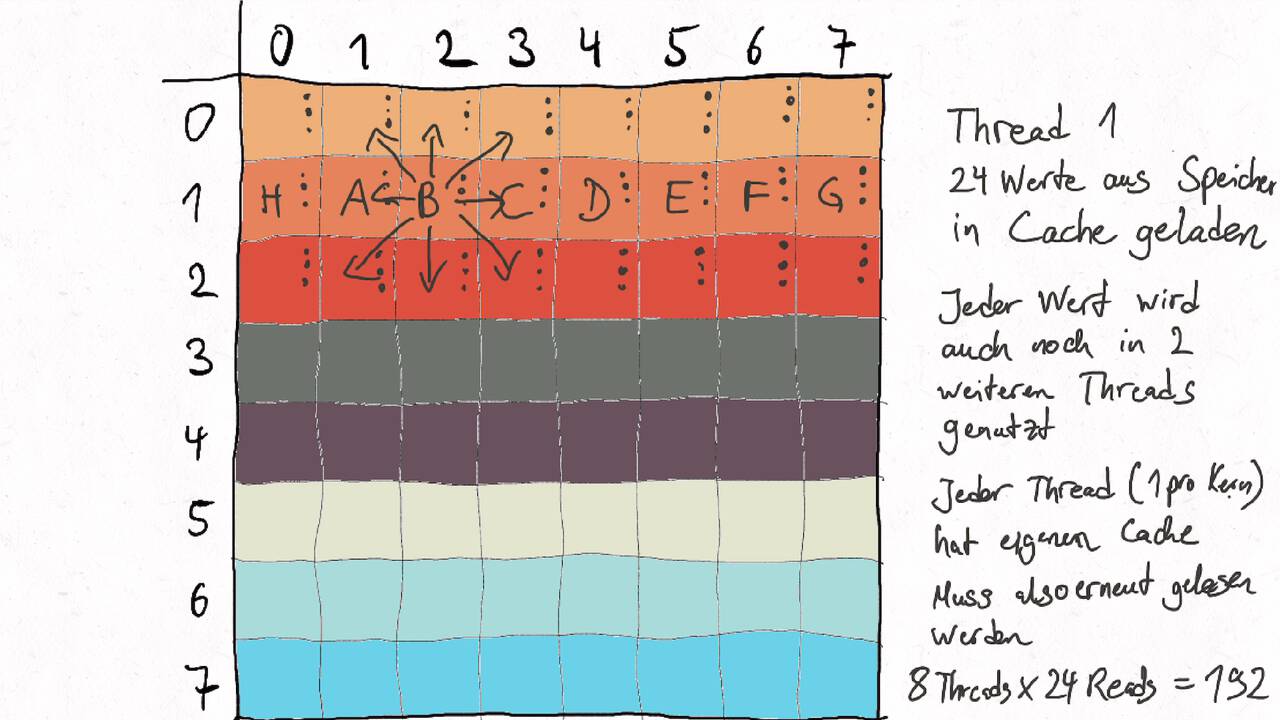
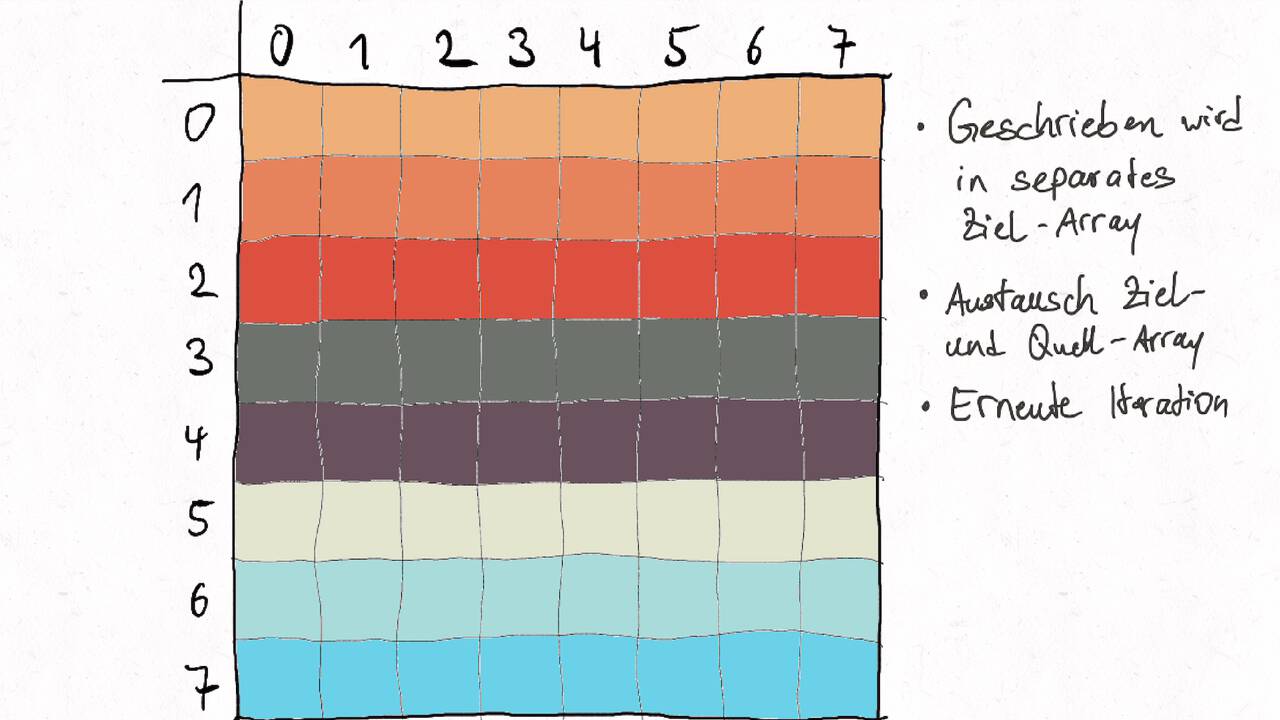
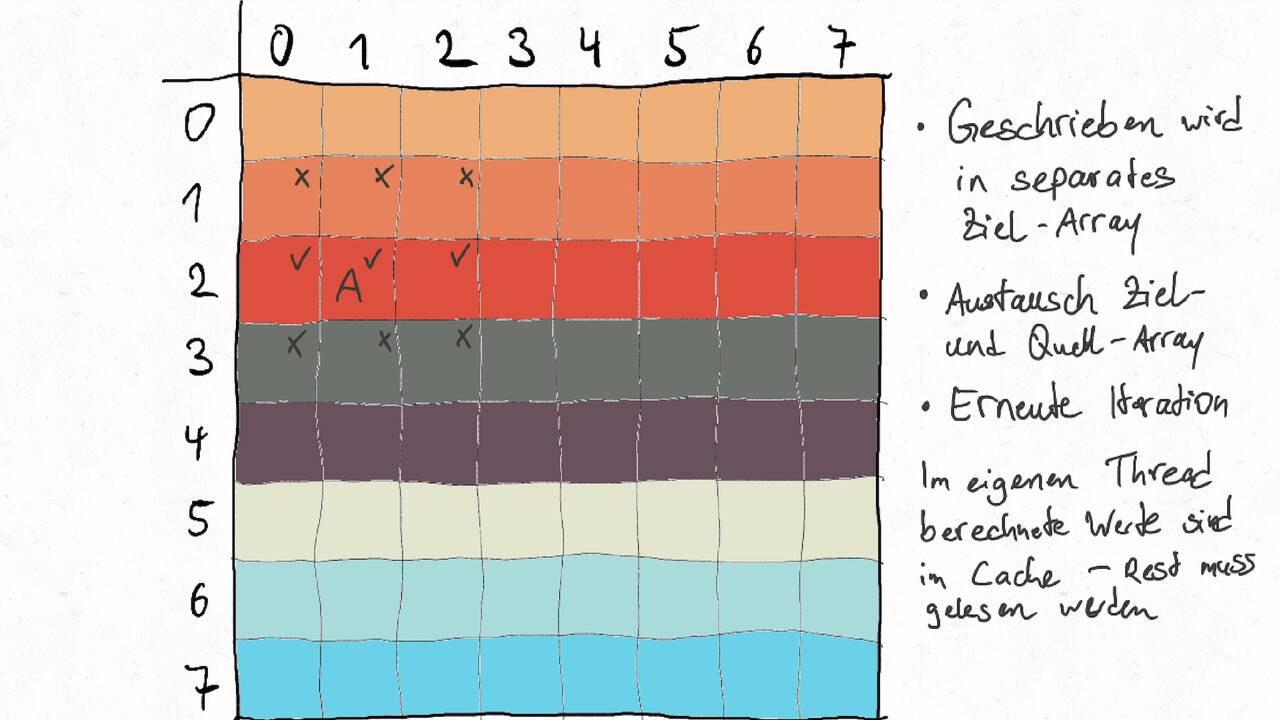
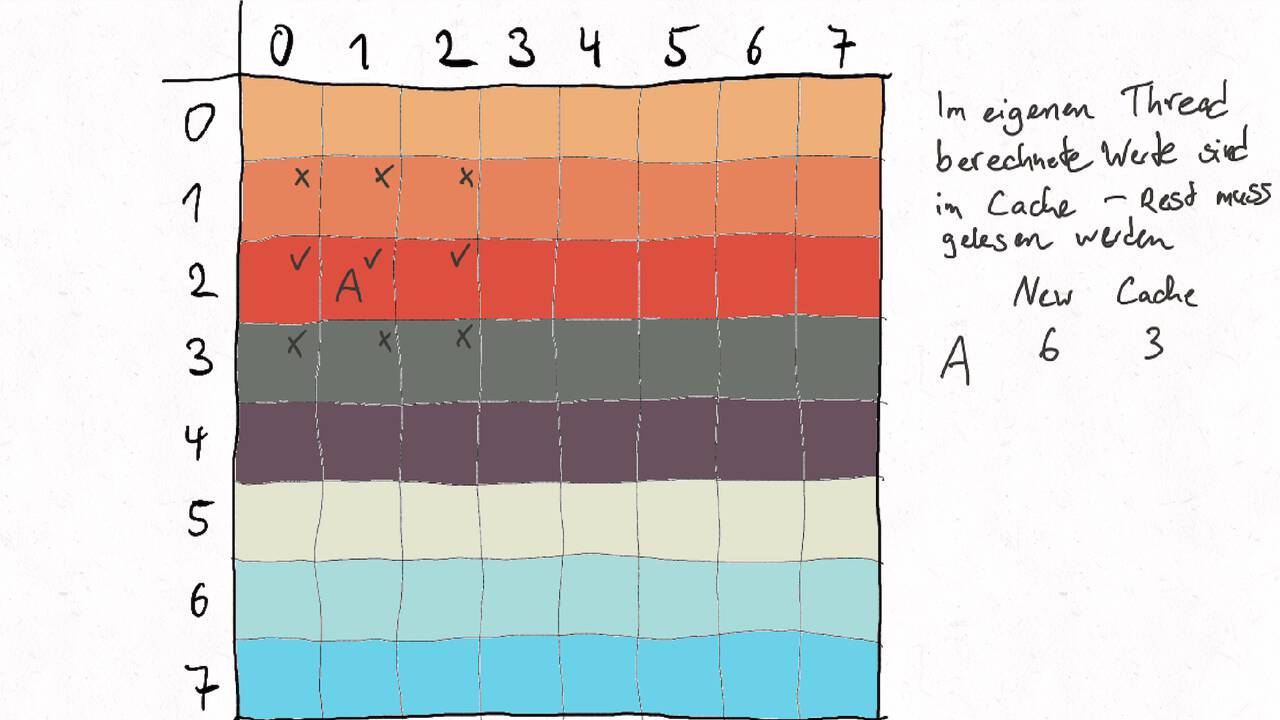
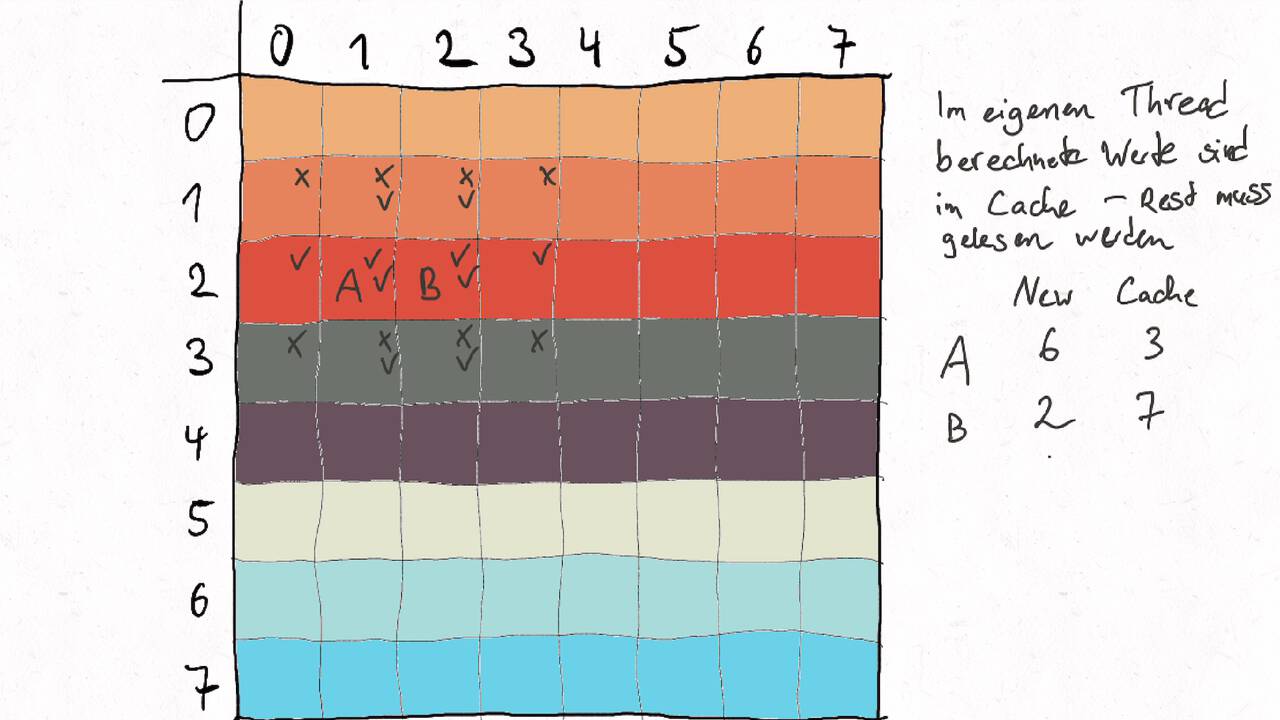
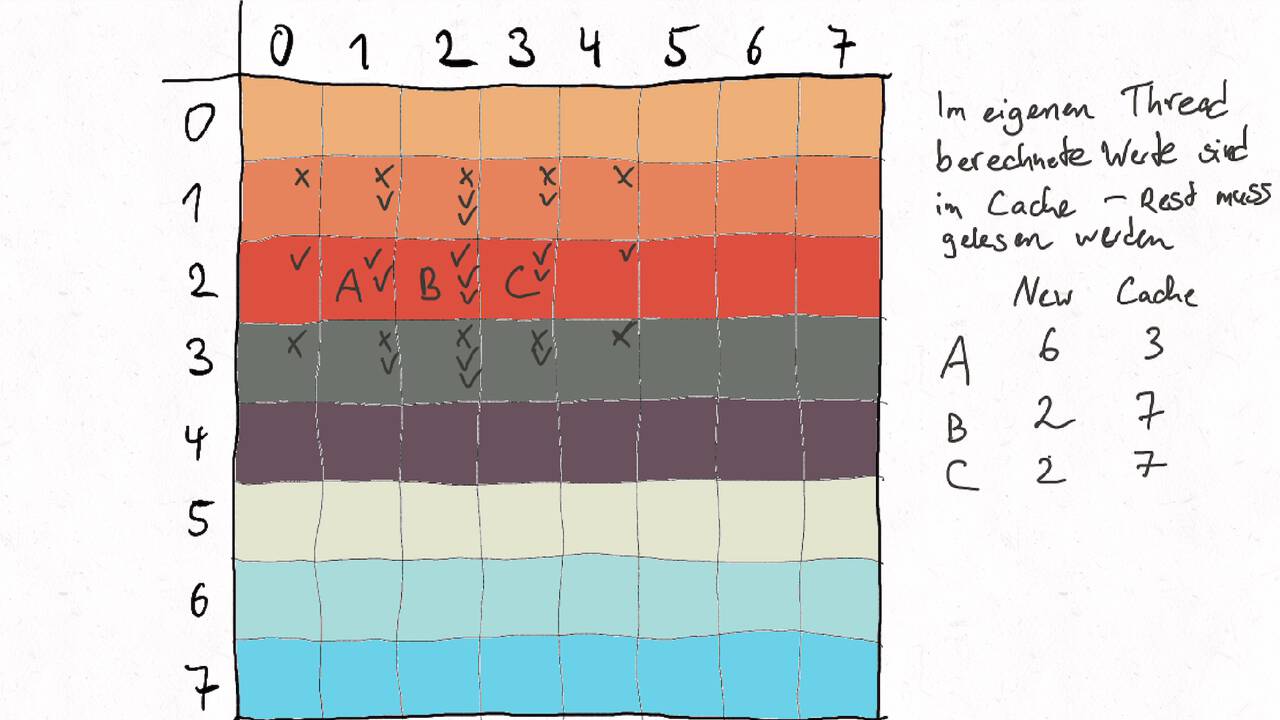
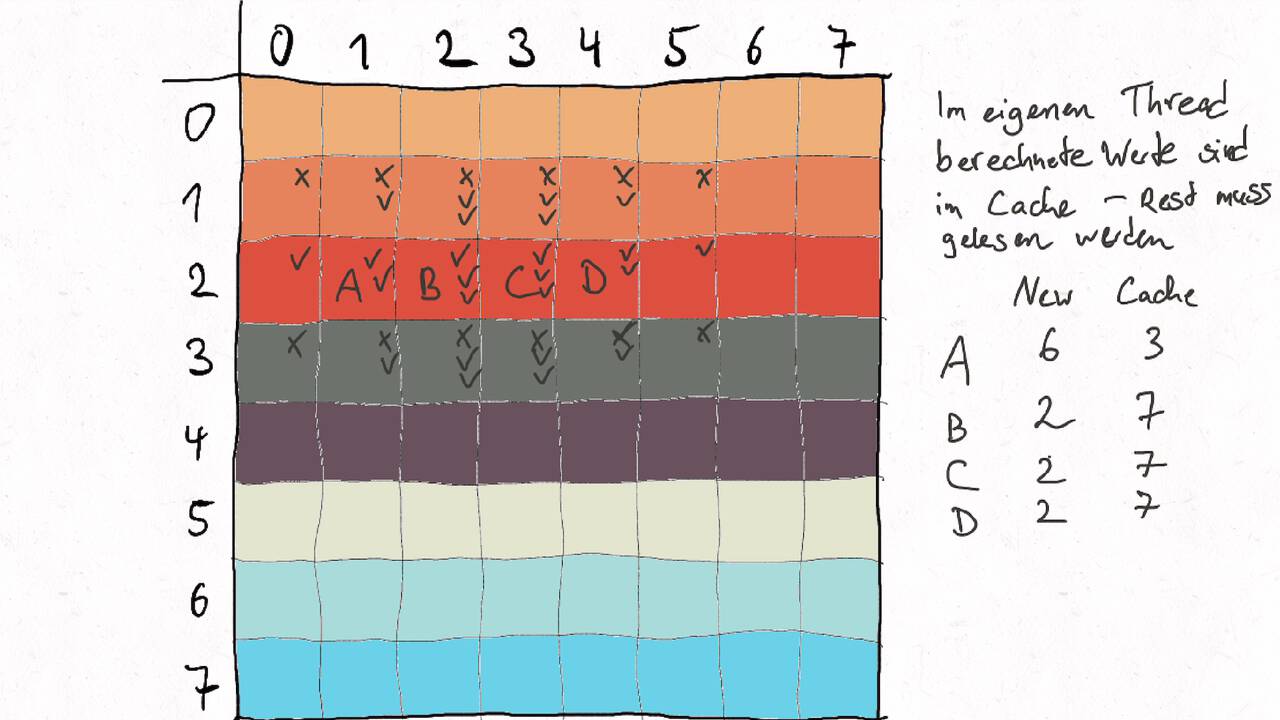
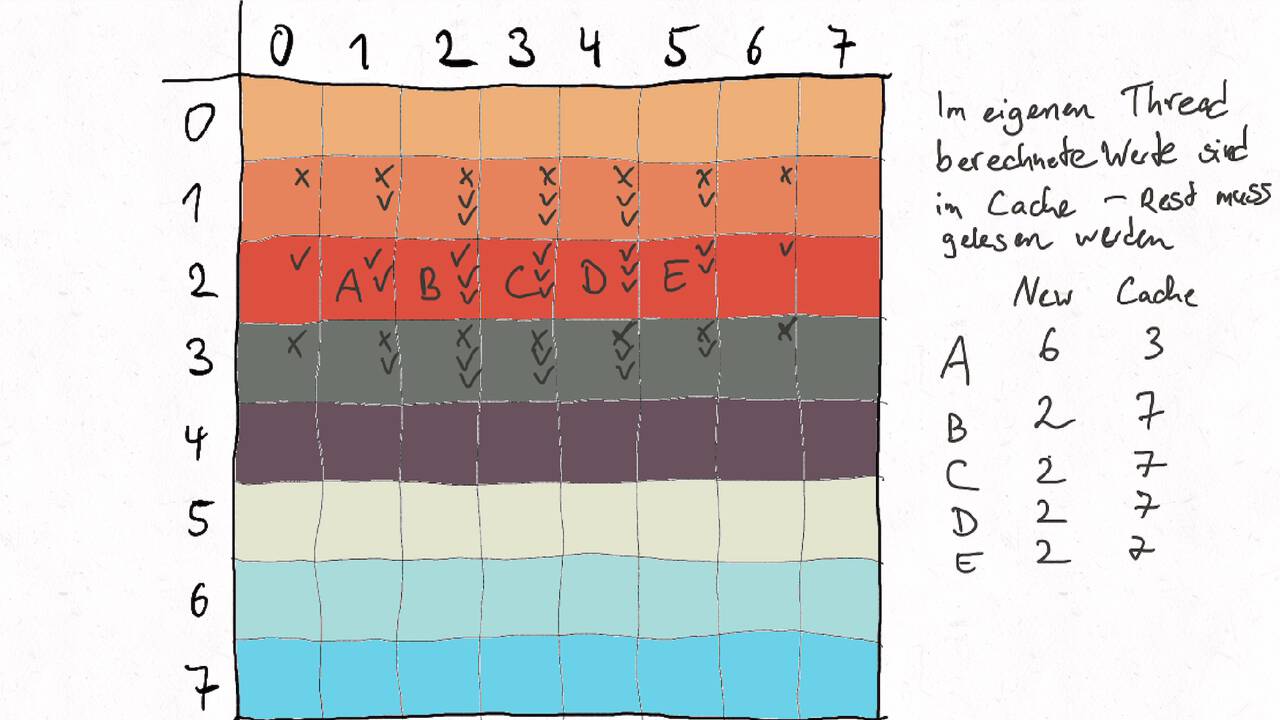
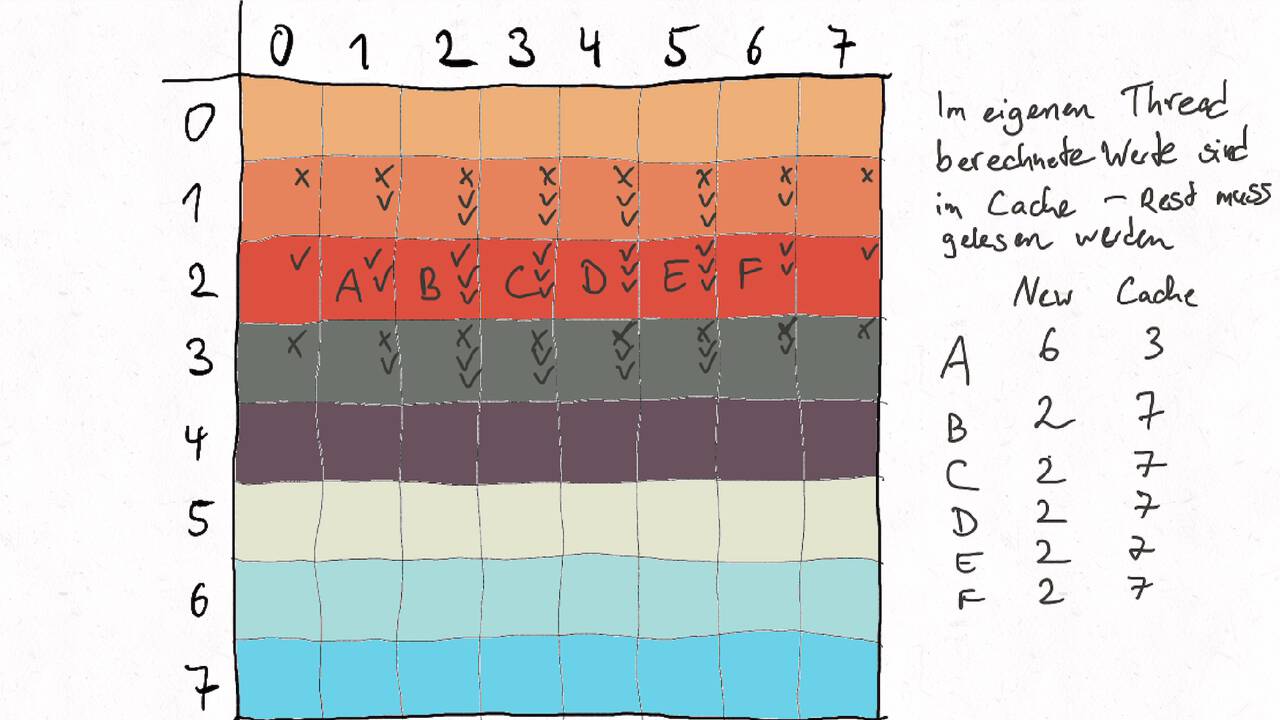
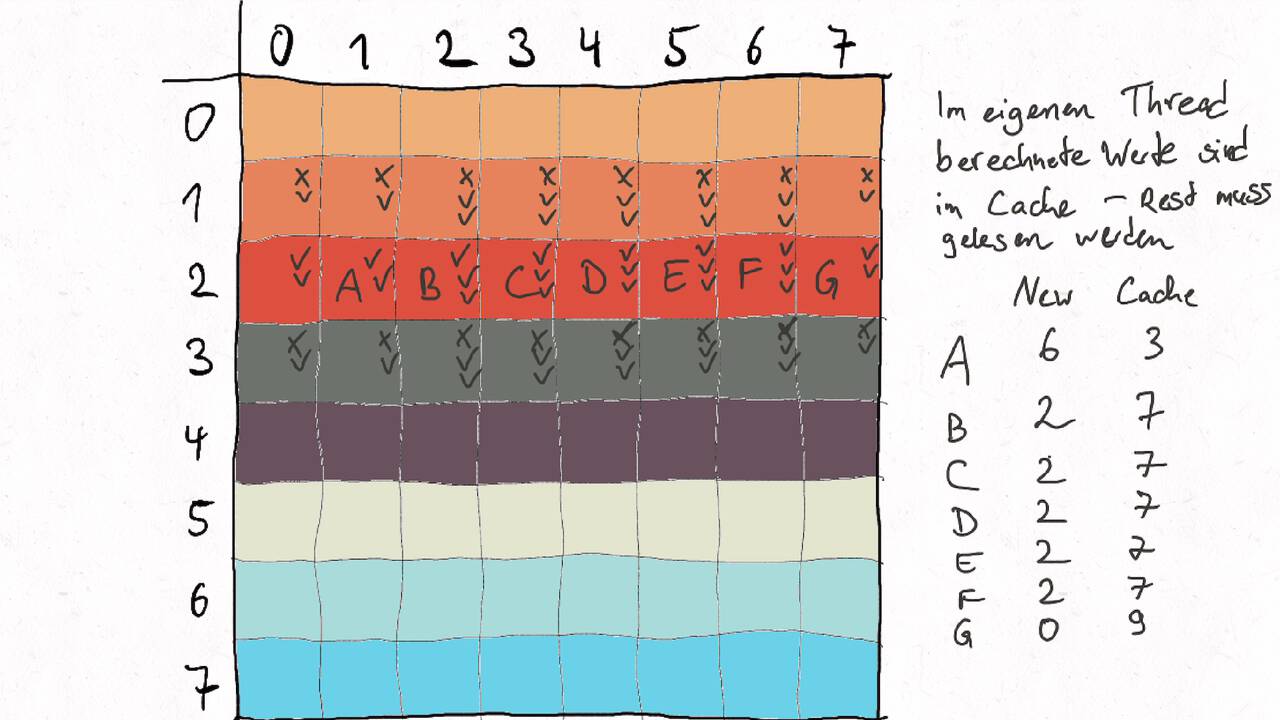
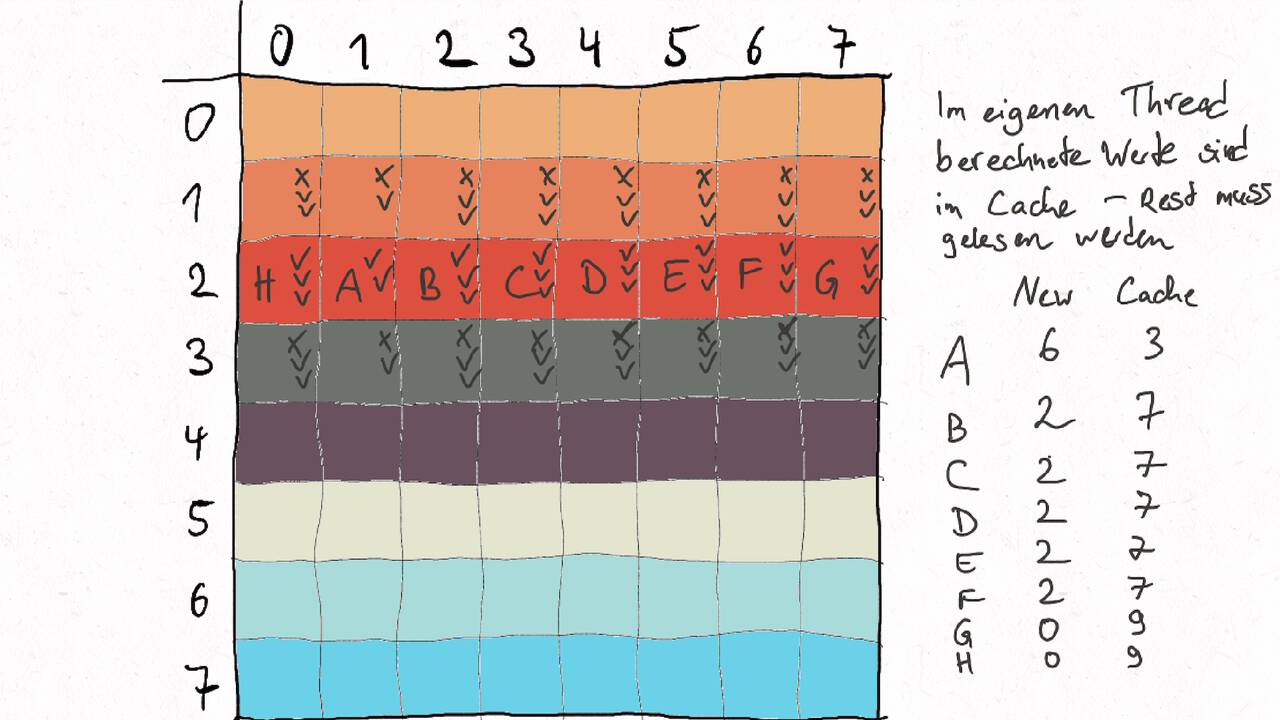
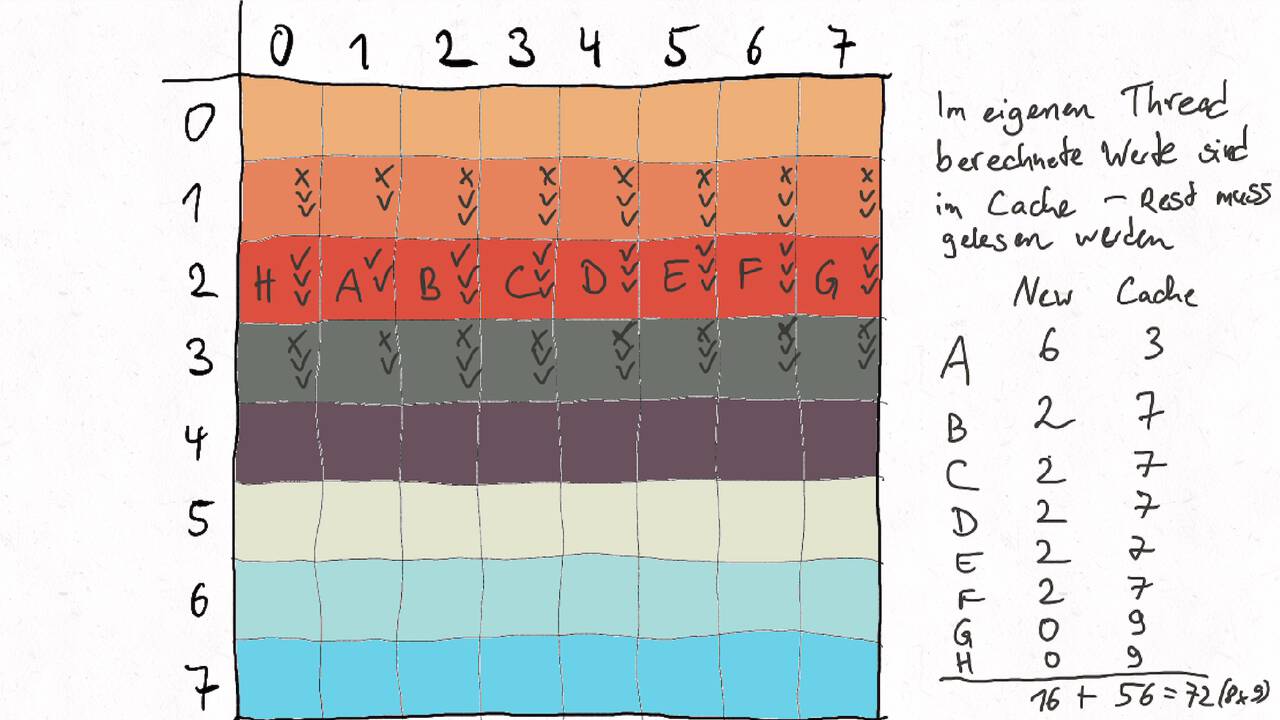
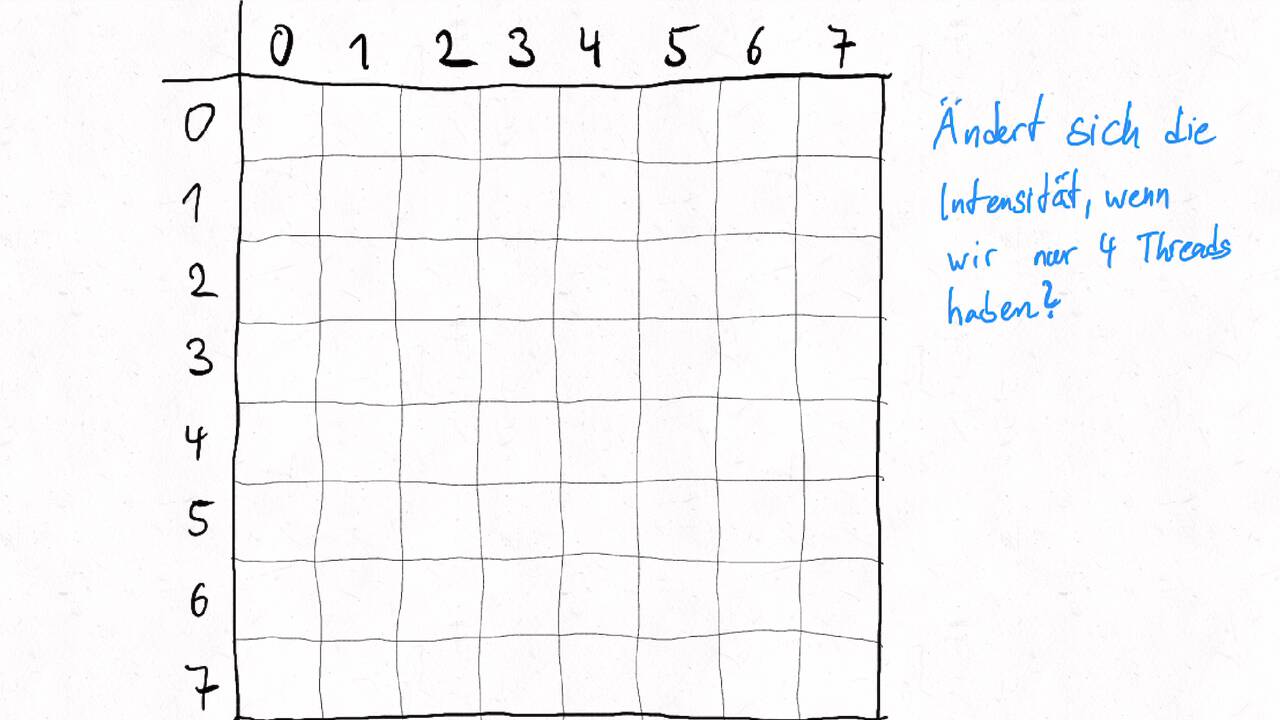
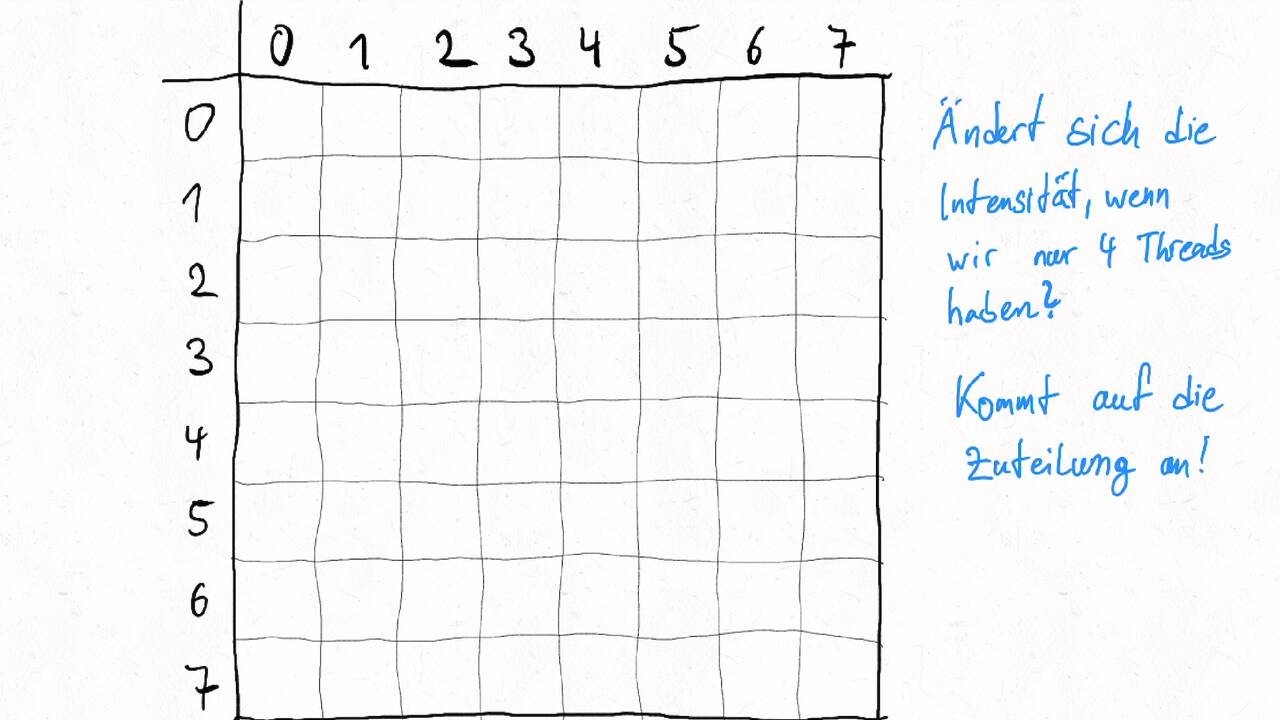
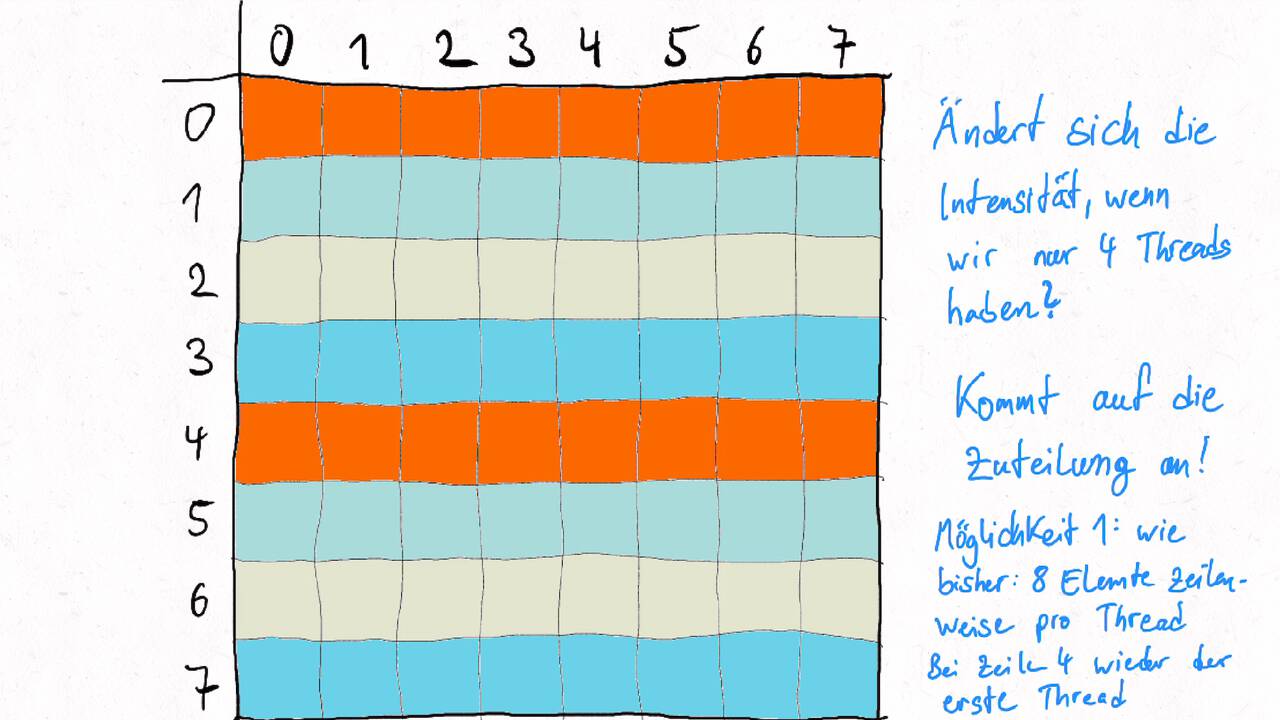
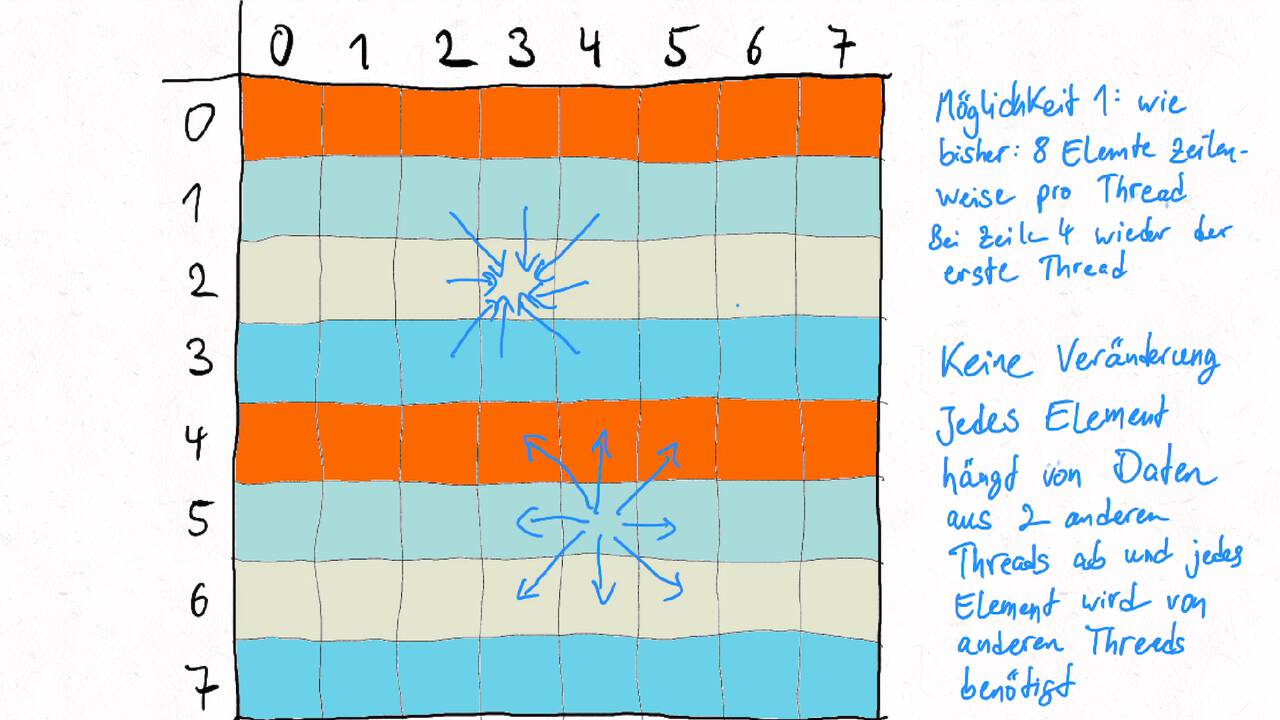
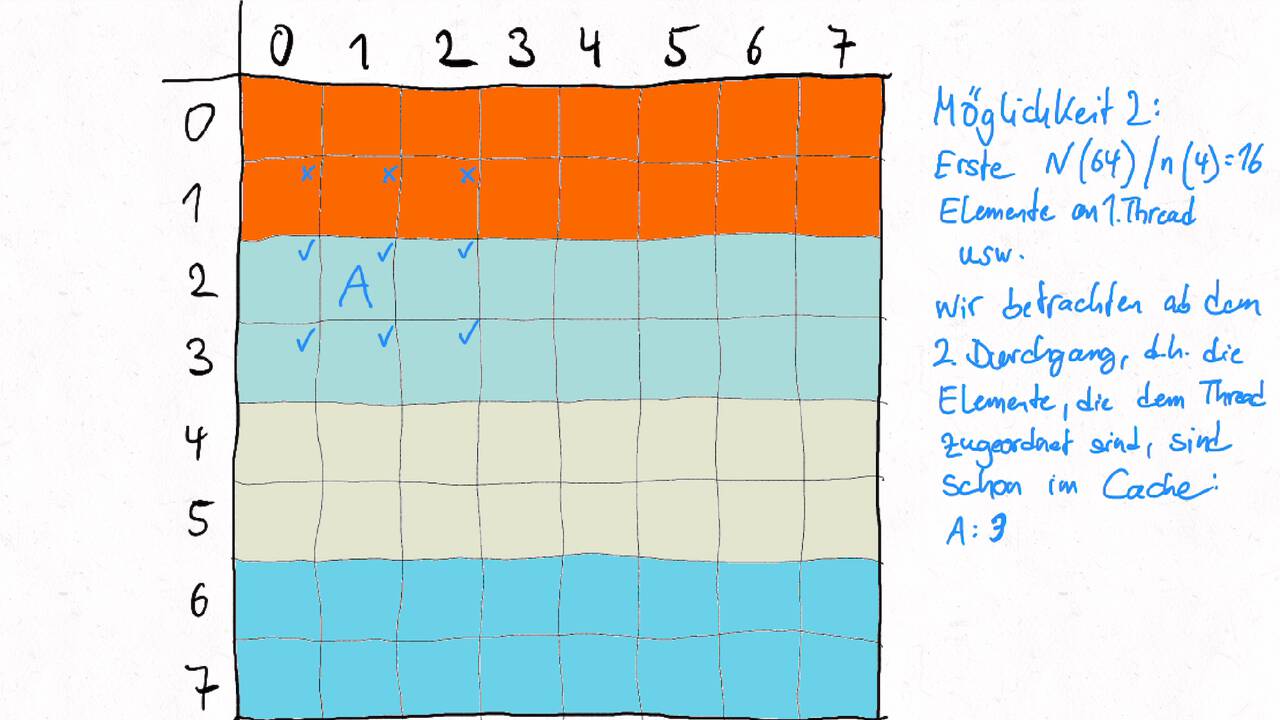
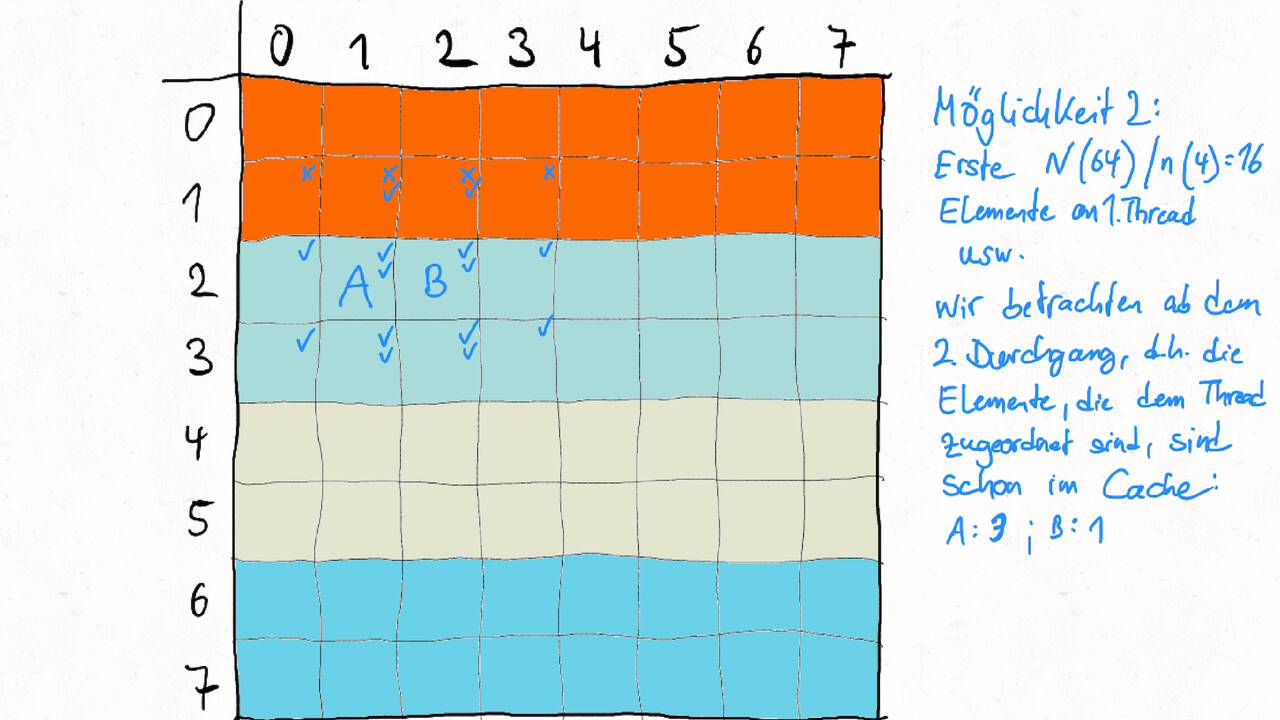
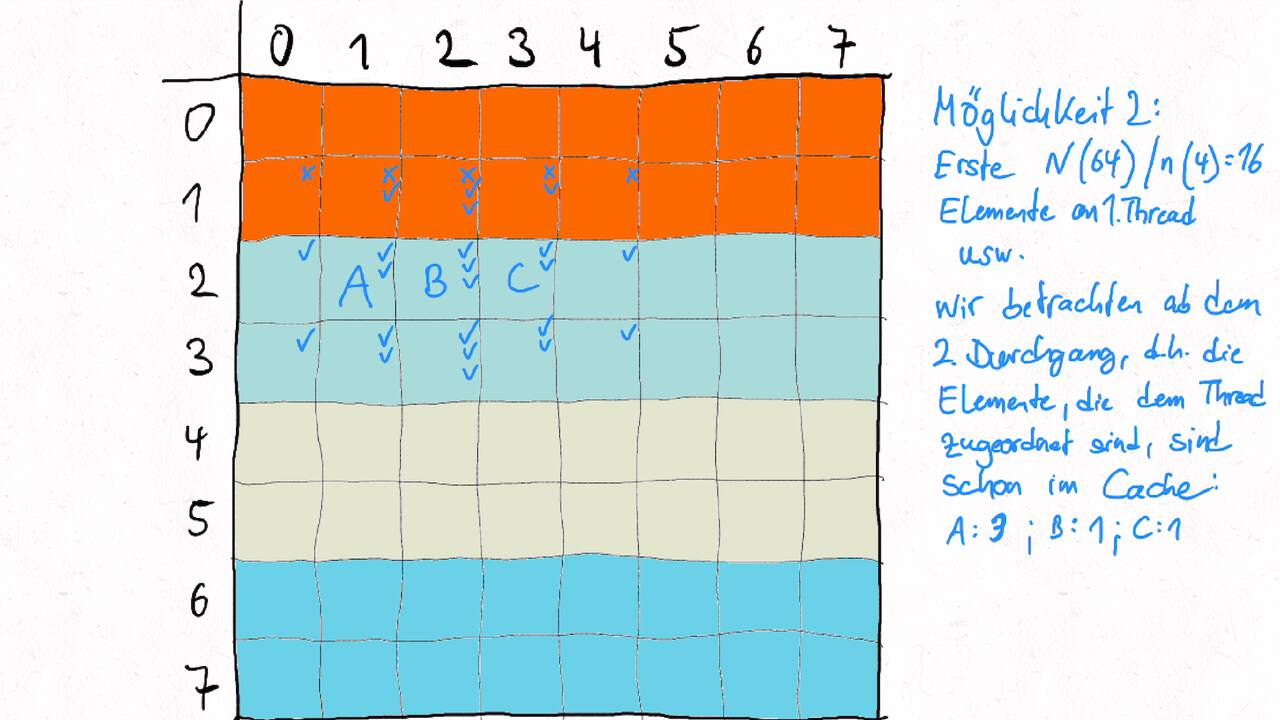
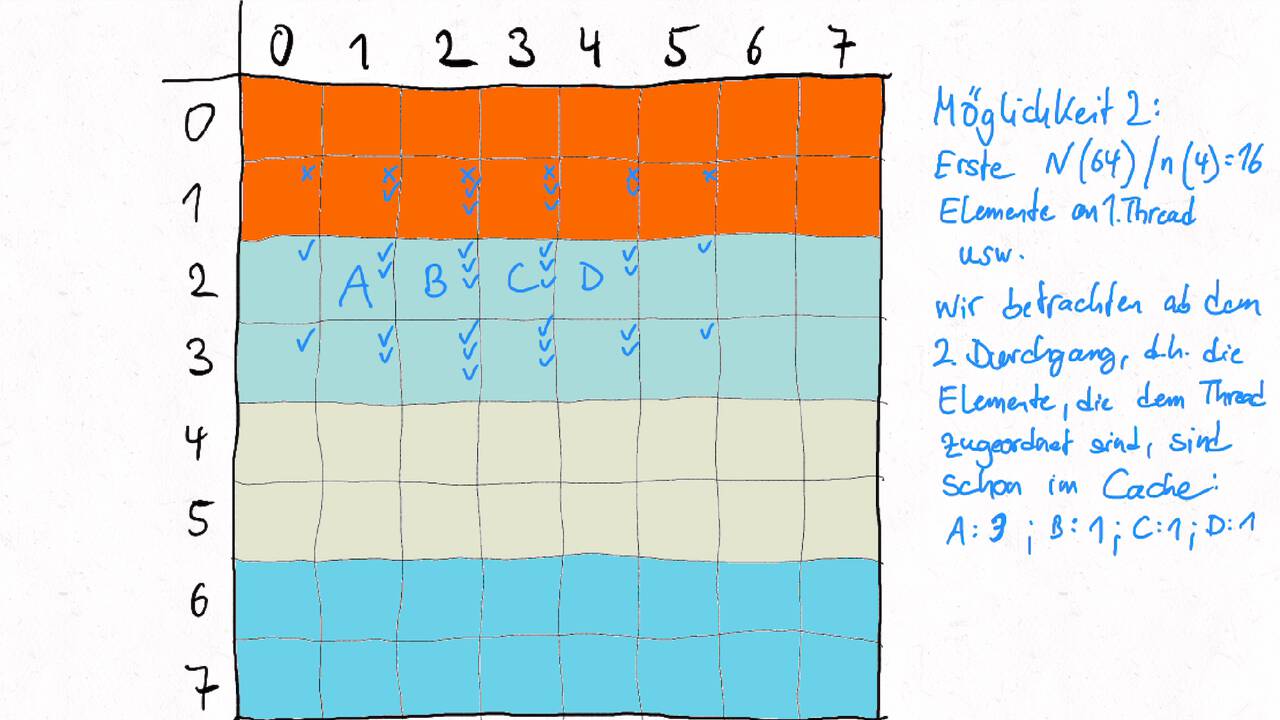
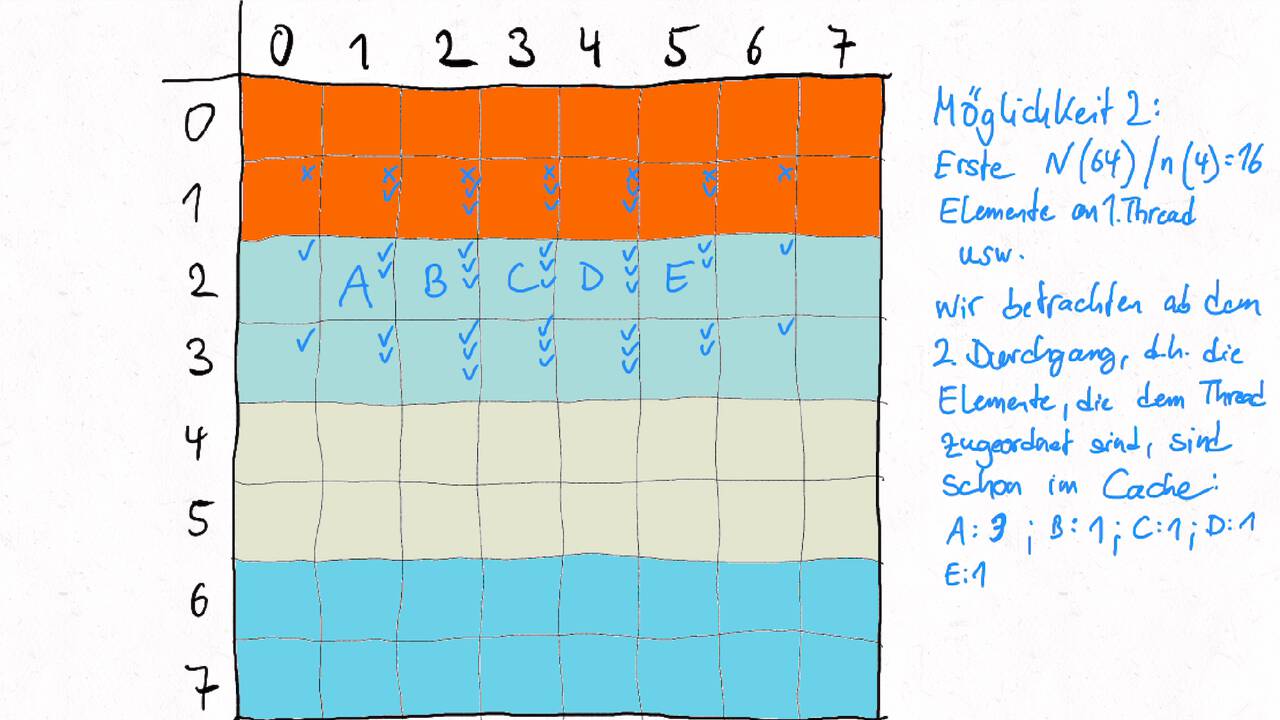
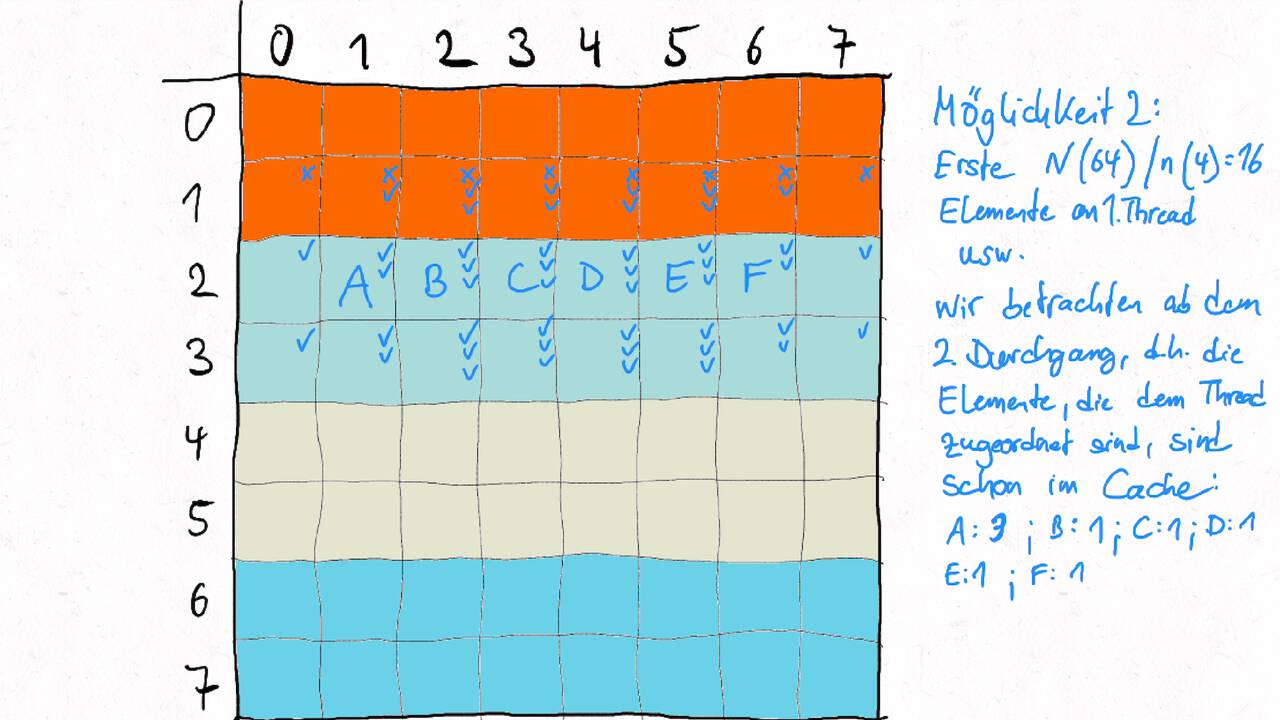
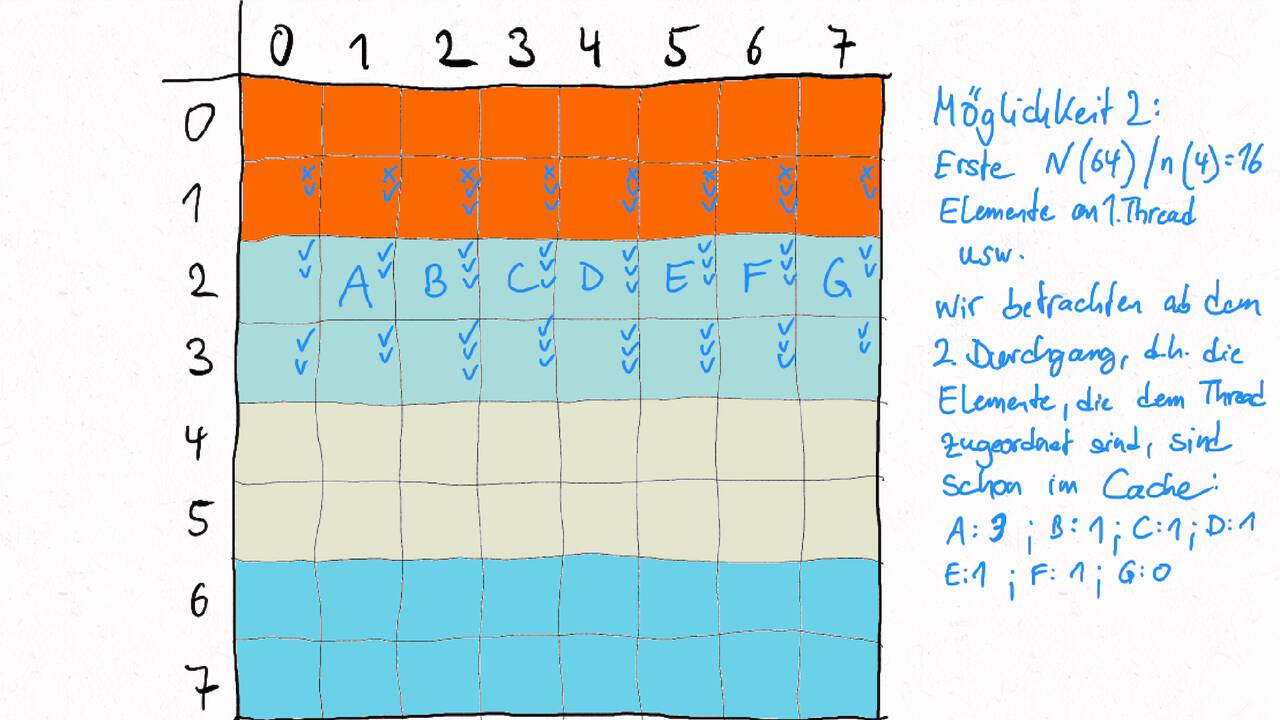
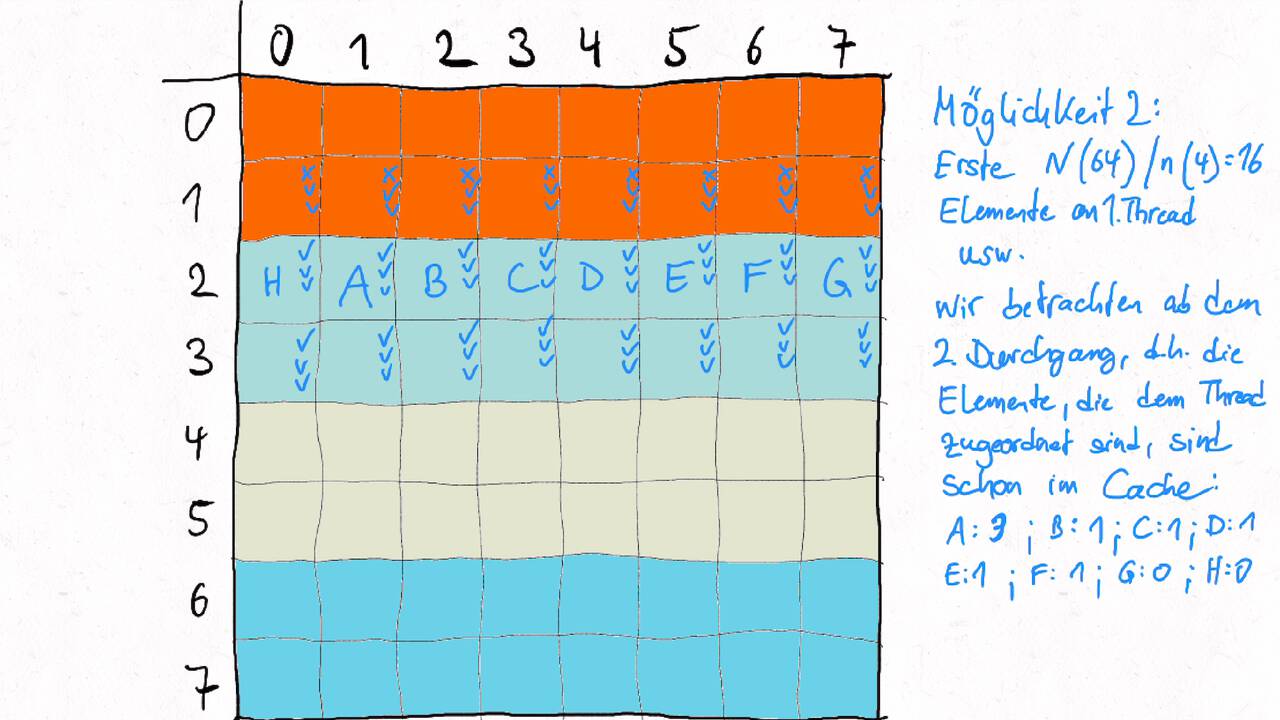
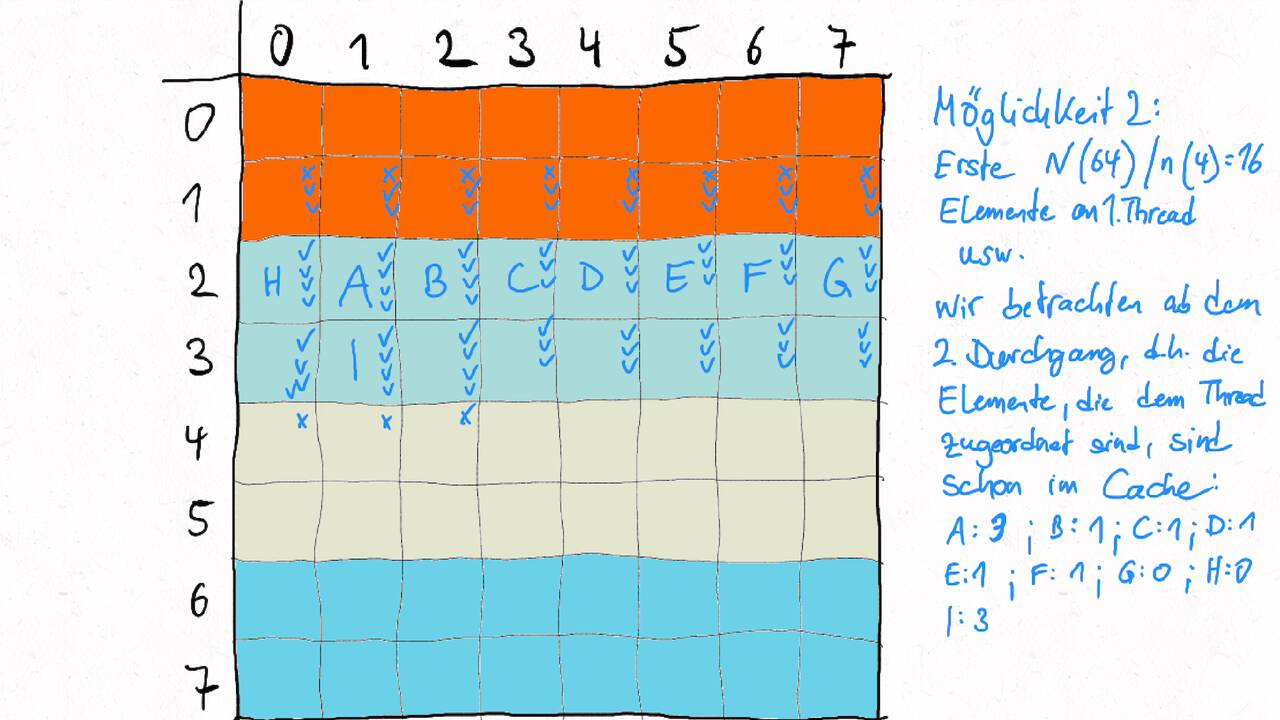
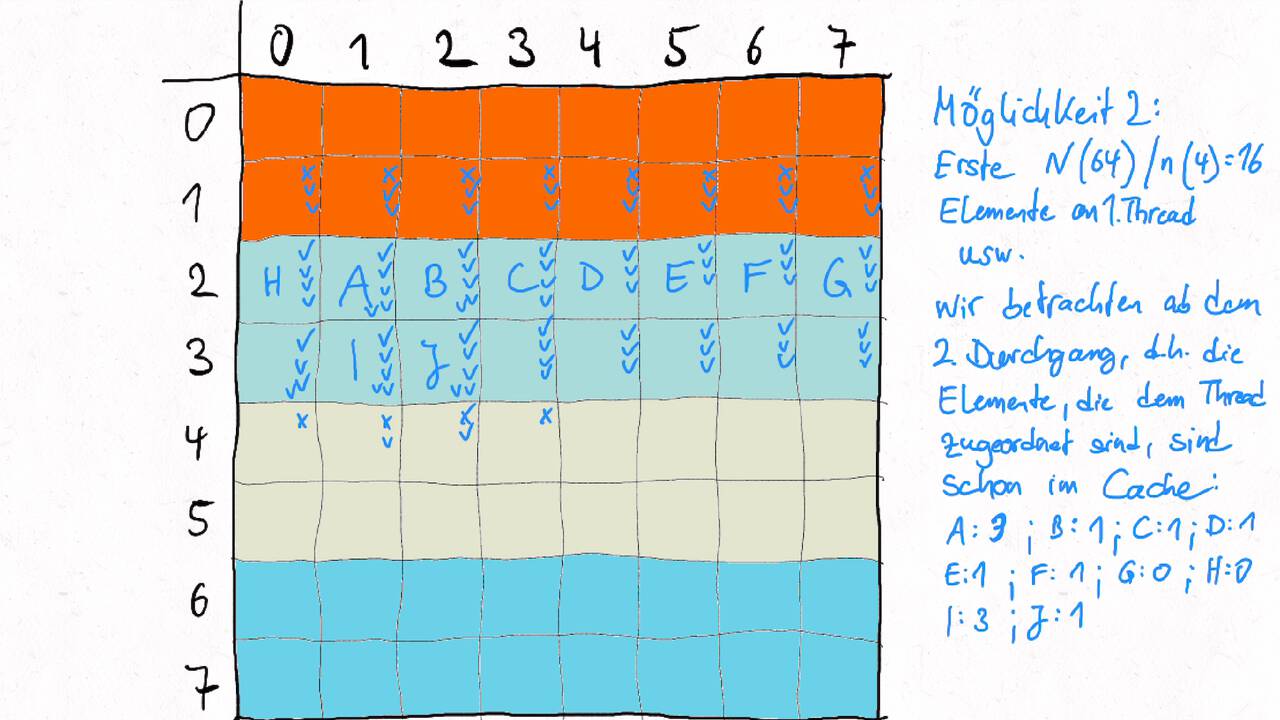
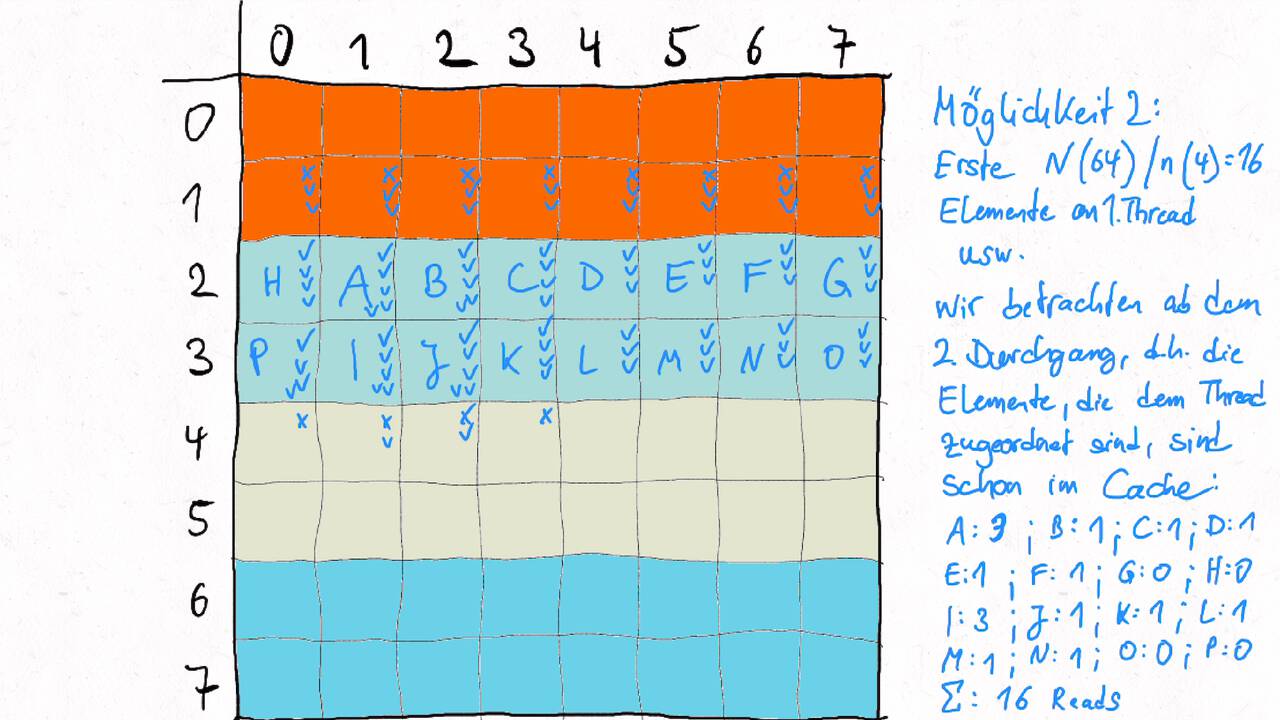
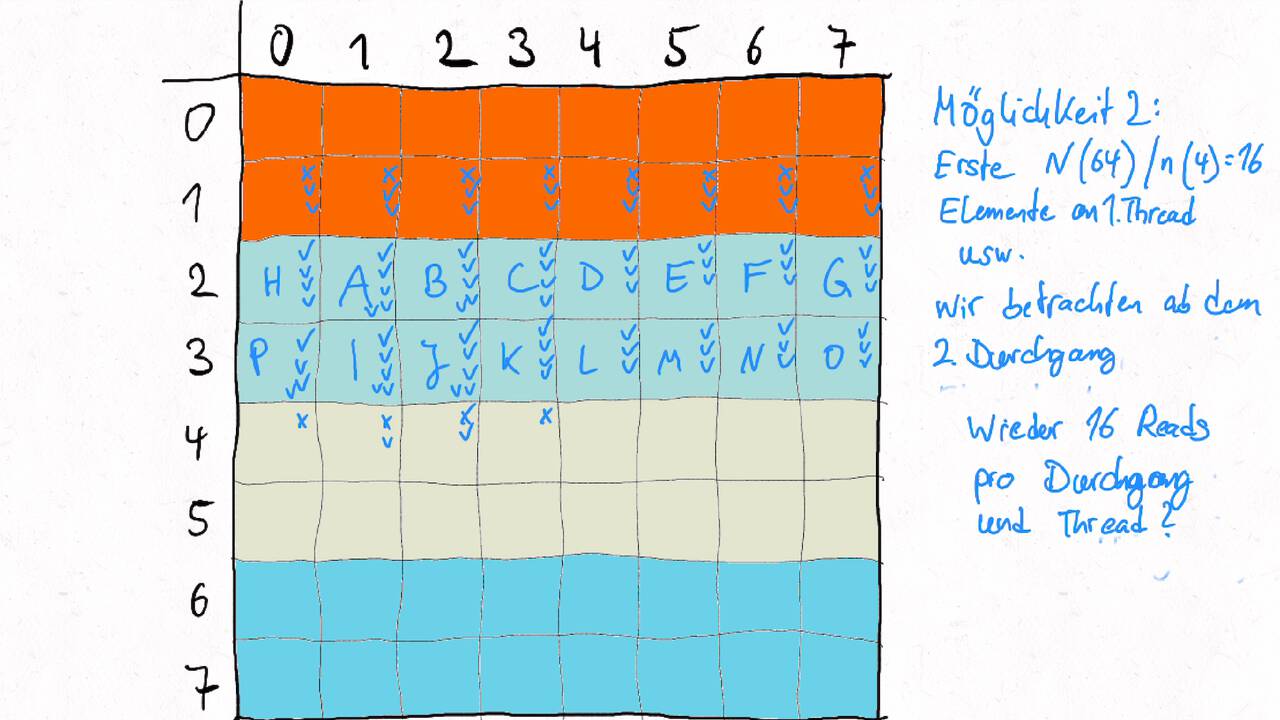
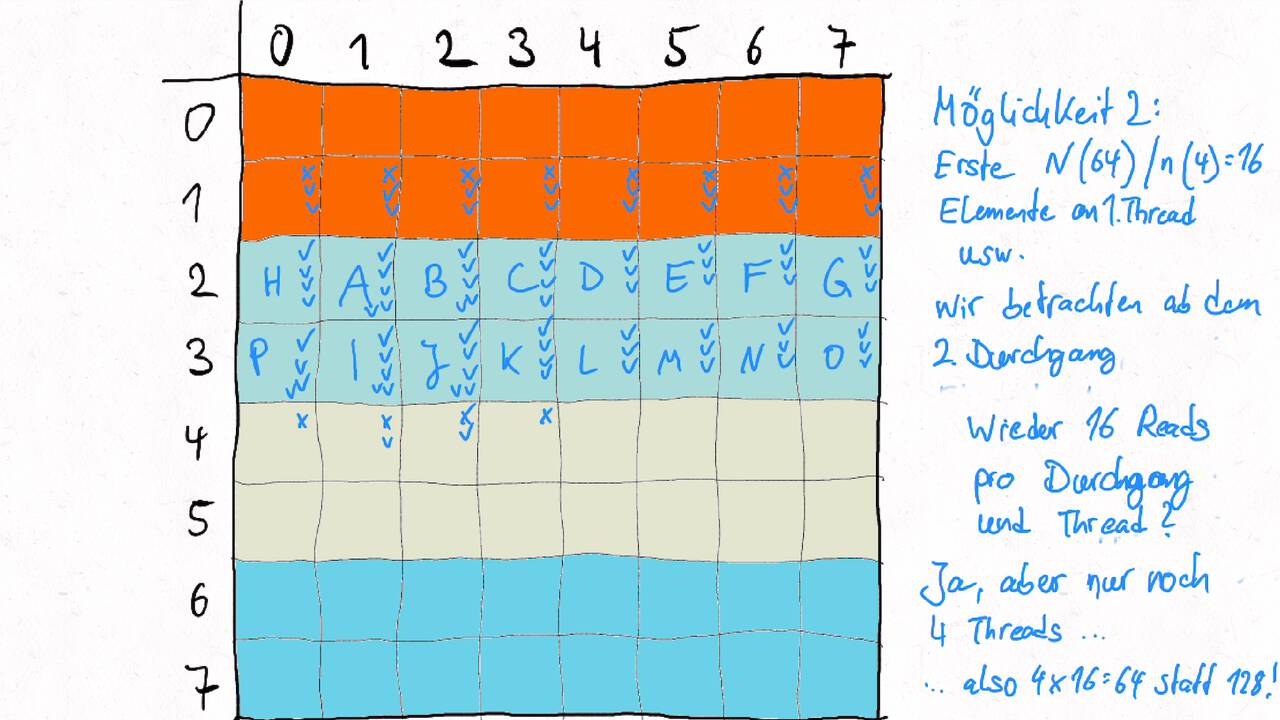
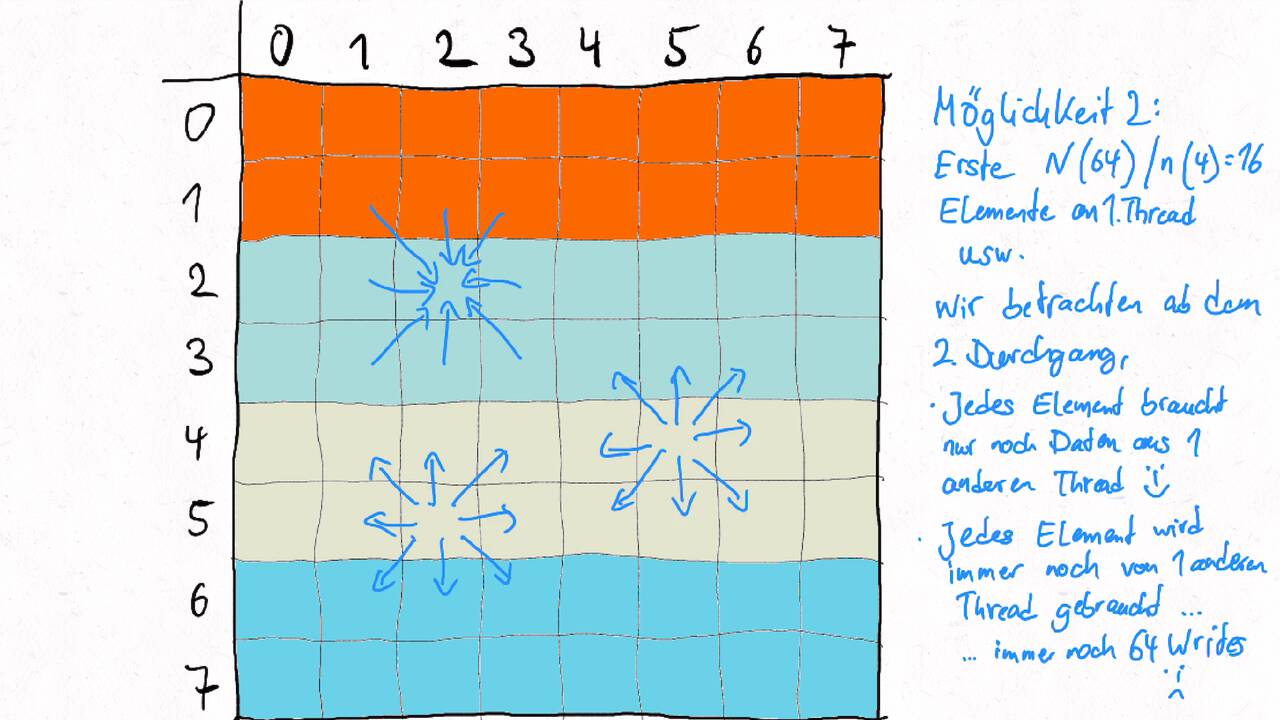
Bestimmen Sie die optimale Arbeitsaufteilung für ein Stencil-Problem.

Als allgemeine Regel lässt sich sagen, dass das Problem so in Teil zerlegt werden soll, dass der Inhalt jedes Teils (bestimmt die Computation) möglichst groß im Verhältnis zur Oberfläche des Teils (bestimmt die Kommunikation) ist.

Im Beispiel oben haben wir uns auf Cache-Hits/-Misses konzentriert. Hier muss natürlich auch die Größe der Caches berücksichtigt werden. Insgesamt ist das Thema der Arbeitsaufteilung auf vielen Ebenen interessant, um Blöcke abzuarbeiten, die möglichst viel Lokal sind. Es kann somit auch zu mehreren Blockebenen kommen, um nacheinander verschiedene Zugriffe zu optimieren:

• Was passt in die Register, in den L1-Cache, in den L2-Cache, in den L3-Cache?

• Was passt in den Hauptspeicher bzw. in verschiedene Hauptspeicherbereiche bei NUMA?

• Was kann auf einem einzelnen Computer berechnet werden - was muss übers Netzwerk ausgetauscht werden?

Die optimalen Blockgrößen hängen stark von der Computerarchitektur ab und können z.B. über Experimente bestimmt werden.

Je nach Problem können unterschiedliche Tiling-Verfahren optimal sein. Diese sind aber oftmals recht komplex, insbesondere , wenn eine diagonale Grenze gezogen wird. Siehe z.B. Diamond-Tiling.

Load Balancing optimieren

Bei der Arbeitsaufteilung der Stencil-Operationen ging es uns vor allem, um die Kommunikationsvermeidung. Der Rechenaufwand bei Stencil ist gleichmäßig verteilt - jedes Element wird auf die gleiche Art und Weise berechnet. Bei der N-Body-Simulation sind die Teil meist ungleichmäßig verteilt. Bei Sternen kommt es zu Häufungen: in Galaxien sind viele Sterne - zwischen Galaxien ist sehr viel leerer Raum. Wenn wir nun den zu simulierenden Raum in gleichmäßige Abschnitte aufteilen, dann wird es Abschnitte mit sehr vielen Objekten geben und leere Abschnitte. Dies führt zu Load Imbalance. Manche Rechenknoten werden sehr lange rechnen, während andere nichts zu tun haben - eine schlechte Auslastung ist die Folge. Stattdessen bietet es sich an, den Raum ungleichmäßig so aufzuteilen, dass Abschnitte mit gleich vielen Elementen entstehen, auch wenn diese dann unterschiedlich groß sind. Bei einem 2D-Raum kann ein Quad-Tree gebildet werden. Die Verteilung muss (hoffentlich möglichst selten) angepasst werden, wenn sich einzelne Objekte aus einem in einen anderen Abschnitt bewegen.

Der Barnes-Hut-Algorithmus nutzt eine solche Aufteilung nicht nur zur Lastverteilung. Es wird darüberhinaus ausgenutzt, dass “Far-Field-Forces”, z.B. die Gravitation in der Sternensimulation, mit steigender Entfernung schwächer werden. In einem einzelnen Abschnitt - hier sind die Sterne nah beinander - wird weiterhin exakt simuliert. Die Kräfte von Sternen in anderen Abschnitten werden angenähert. Hierzu werden alle Sterne in einem Abschnitt zusammengefasst in ein Objekt mit der gewichteten Position und der Gesamtmasse. Nun werden nur noch die Kräfte zwischen den Abschnitten simuliert. Insgesamt ergibt sich eine Reduktion der Komplexität von \(n^2\) (jeder Stern muss mit jedem anderen Stern abgeglichen werden) zu \(n * \log(n)\) (jeder Stern wird mit den Sternen im gleichen Abschnitt und den anderen Abschnitten abgeglichen).

Optimierung des Synch-Overheads

Simulationen verfügen manchmal über Teilaspekte, die zwar verbunden sind aber die Wechselwirkungen zwischen den Teilaspekten schwächer/seltener sind als innerhalb der Teilaspekte. Ein Beispiel wäre eine Klimasimulation mit den Aspekten Ozeane und Landmassen. Als Vereinfachung betrachten wir ein Game-of-Life mit folgender Struktur:

Fig. 7 Schwach verbundene Teilprobleme

Realistisch wären die einzelnen Teilfelder (blau, grün, rot) größer aber was wir sehen, die Teilfelder sind nur über dünne Verbindungen (gelb) in Wechselwirkung. Die Bildung/das Verschwinden von Elementen in jedem Teilfeld hängt von den Nachbarn ab, also vor allem von den anderen Elementen im gleichen Teilfeld. Nur in wenigen Fällen wird es eine relevante Änderung in einem gelben Verbindungsfeld geben. Im Standardvorgehen wird dennoch nach jedem Zeitschritt synchronisiert, d.h. es wird gewartet bis alle neuen Elemente berechnet wurden. Es wird auch immer das gesamte Feld simuliert, auch wenn z.B. ein Teilfeld komplett leer ist.

Alternativ können die Teilfelder unabhängig voneinander simuliert werden. In anderen Arten von Simulationen wären z.B. unterschiedlich große Zeitschritte denkbar. Zur Synchronisation sind zwei Methoden denkbar:

• Konservativ: jedes Teilfeld wird nur so weit simuliert, wie bekannt ist, dass die anderen Teilfelder keinen Einfluß haben können

• Spekulativ/Optimistisch: jedes Teilfeld wird weiter simuliert unter der Annahme, dass von den anderen Teilfelder kein neuer Einfluß kommt. Wenn ein externer Einfluß für einen vorherigen Simulationsschritt kommt, dann werden die seither generierten Schritte verworfen und neu berechnet.

Mehrarbeit durch Parallelisierung

Die Präfix-Summe (Prefix-Sum, Scan, Cumulative Sum) ist ähnlich einer Reduce-Operation mit Summe, nur dass alle Zwischenergebnisse gespeichert werden (siehe oben). Die Präfix-Summe hat viele Anwendungen, z.B. beim parallelen Sortieren oder der Arbeitsaufteilung - für eine tiefergehende Betrachte siehe “Prefix Sums and Their Applications” von Guy E. Blelloch. Ebenso wie Reduce lässt sich diese sequenzielle Aufgabe dank Assoziativität parallelisieren. Dabei gibt es verschiedene Möglichkeiten vorzugehen. Die folgende Beschreibung und Graphiken basieren auf dem Wikipedia-Artikel zu Prefix-Sum in der Version vom 29.10.2021. Dabei ist jeweils eine Mehrarbeit notwendig gegenüber den n Rechenoperationen, die beim sequenziellen Algorithmus notwendig sind.

Möglichkeit 1: Hillis-Steele

Fig. 8 Hillis-Steele Prefix-Sum. Darstellung von Scott Pakin, 2018, abgerufen am 29.10.2021 von https://en.wikipedia.org/wiki/File:Hillis-Steele_Prefix_Sum.svg

Der Span des DAGs (\(T_\infty\)) beträgt hier 4 für ein Array mit 16 Elementen. Generell: \(\log_2(n)\) für ein Array mit n Elementen.

Möglichkeit 2:

Fig. 9 Arbeitseffiziente parallele Prefix-Sum. Darstellung von David Eppstein, 2011, abgerufen am 29.10.2021 von https://en.wikipedia.org/wiki/File:Prefix_sum_16.svg

Der Span des DAGs (\(T_\infty\)) beträgt hier 6 für ein Array mit 16 Elementen. Generell: \(2\log_2(n) - 2\) für ein Array mit n Elementen.

Beide Möglichkeiten erfordern also \(O(\log(n))\) Zeit. Die Unterschiede:

• Möglichkeit 2 benötigt doppelt so lange, wenn man die O-Notation außen vor lässt

• Möglichkeit 1 benötigt \(O(n\log(n))\) Operationen und Möglichkeit 2 \(O(n)\) Operationen Das heißt in Konsequenz, dass Möglichkeit 1 schneller ist aber nur wenn genügend Prozessoren verfügbar sind, um die höhere benötigte Anzahl von Operationen auszugleichen